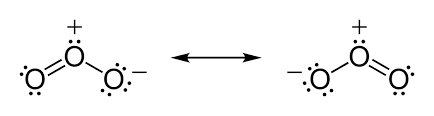
 ஒரே மூலக்கூறு அல்லது அயன் கூட்டத்தில் இலத்திரன் ஒழுங்கு அமைப்பின் மாற்றங்களின் அடிப்படையில் மாத்திரம் வேறுபடும் லூயியின் கட்டமைப்புக்கள் இரண்டு அல்லது அதற்கு மேற்பட்ட எண்ணிக்கை கொண்ட சந்தர்ப்பங்கள் உண்டு. குறித்த ஒரு மூலக்கூறின் அவ்வாறான கட்டமைப்புக்கள் பரிவுக் கட்டமைப்புக்கள் எனப்படும். எனினும் குறித்த மூலக்கூறின் உண்மையான கட்டமைப்பு இக்கட்டமைப்புகளில் ஒன்றாக அமையாது. மாறாக பரிவுக்கட்டமைப்புக்கள் கலப்புற்று உருவாகும் உறுதித்தன்மை மிக்க மற்றொரு கட்டமைப்பாக அமையும்.
ஒரே மூலக்கூறு அல்லது அயன் கூட்டத்தில் இலத்திரன் ஒழுங்கு அமைப்பின் மாற்றங்களின் அடிப்படையில் மாத்திரம் வேறுபடும் லூயியின் கட்டமைப்புக்கள் இரண்டு அல்லது அதற்கு மேற்பட்ட எண்ணிக்கை கொண்ட சந்தர்ப்பங்கள் உண்டு. குறித்த ஒரு மூலக்கூறின் அவ்வாறான கட்டமைப்புக்கள் பரிவுக் கட்டமைப்புக்கள் எனப்படும். எனினும் குறித்த மூலக்கூறின் உண்மையான கட்டமைப்பு இக்கட்டமைப்புகளில் ஒன்றாக அமையாது. மாறாக பரிவுக்கட்டமைப்புக்கள் கலப்புற்று உருவாகும் உறுதித்தன்மை மிக்க மற்றொரு கட்டமைப்பாக அமையும்.