• The solubility of NaCl in water is approximately 5 mol dm^-3. In the solution there are interactions between Na⁺ and Cl^– ions. Though simple, they are not independent of one another.

• In the case of a sparingly soluble electrolyte such as BaSO₄, the ions exist independently in the solution and the following dynamic equilibrium exists between the solid and the ions in a saturated solution.

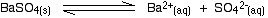
Applying the law of equilibrium

[BaSO₄(s)] is a constant. Therefore,

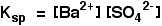
• Ksp is a constant at constant temperature and is called ‘solubility product’. If the solubility of BaSO₄ is x mol dm^-3, Ksp = x² mol² dm^-6.

• In general, solubility product is not applied for salts having high solubility.

• If the ionic product is greater than the solubility product of a salt, it will precipitate.
eg. If [Ba²⁺][SO₄^2-] > Ksp   BaSO₄ will precipitate.

Example

The solubility of magnesium hydroxide at 298 K is 1.71 x 10^-4mol dm^-3. Calculate the solubility product.

The equilibrium is:

For every mole of magnesium hydroxide that dissolves, you will get one mole of magnesium ions, but twice that number of hydroxide ions.

So the concentration of the dissolved magnesium ions is the same as the dissolved magnesium hydroxide:

[Mg²⁺] = 1.71 x 10^-4 mol dm^-3

The concentration of dissolved hydroxide ions is twice that:

[OH^–] = 2 x 1.71 x 10^-4 = 3.42 x 10^-4 mol dm^-3

Now put these numbers into the solubility product expression and do the sum.

Common ion effect

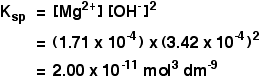
• On addition of NaCl solution to a saturated solution of AgCl, concentration of Cl^– ions increases. Since Ksp is a constant at constant temperature Ag⁺ concentration in the medium should decrease. Therefore, AgCl is precipitated. In other words, the solubility of AgCl in a solution ofup> ions is less compared to its solubility in pure water. This is called common ion effect. This principle is applicable for the Ag⁺ ion as well.