Consider a chemical reaction

aA + bB → cC + dD

rate with respect to the change of concentration of the reactant A = – Δ[A]/Δt

rate with respect to the change of concentration of the product D = Δ[D]/Δt

• In a given reaction, the rates of removal of each reactant and rates of formation of each products are not equal.

• The rate of removal of a reactant or formation of a product depends on the stoichiometric coefficients of the respective substances.

rate of reaction = – (1/a)Δ[A]/Δt      =  -(1/b)Δ[B]/Δt     =  (1/c)Δ[C]/Δt   = (1/d)Δ[D]/Δt

• Rate law for the above generalized equation = k [A] x [B] y, where x and y are
order of reaction with respect to reactants A and B respectively.
• (x + y) of the above expression is referred as the overall order of the reaction.

Example 

Express the rate of the reaction given, in terms of reactants and product concentrations.

The rate of the reaction is expressed as

Zero order reaction

 Ammonia (NH₃) gas decomposes over platinum catalyst to nitrogen gas (N₂) and hydrogen gas (H₂). The chemical reaction is as follows:

The reaction follows zero order kinetics. Therefore the rate law is rate r = k[NH₃]^o

For a zero order reaction the concentration versus time profile is linear and the rate of reaction versus time has the profile.

Concentration versus time profile for a zero order reaction

 Rate of reaction versus time for a zero order reaction

First order reaction

Cyclopropane (C₃H₆) at room temperature has a ring structure. When it is heated, the ring opens up and cyclopropane isomerizes to propylene.

The reaction takes place in a first order manner. Therefore, the rate law for the reaction is, rate (r) = k [C₃H₆]¹

First Order Reaction: Concentration versus time profile

The above figure is an example of the first order reaction. The rate of the reaction depends on the concentration of the reactant. Initially the rate is fast and then it slows down as the concentration of the reactant falls.

Second order reaction

Nitrogen dioxide (NO₂) gas reacts with fluorine gas (F₂) to give nitrosyl fluoride. The chemical reaction is given by the equation.

The reaction has the rate law as:

rate (r) = k [NO₂] [F₂]

The rate has order one with respect to nitrogen dioxide concentration and fluorine concentration and the overall order is (1 + 1) which is two.

This depicts the change of concentration of second order reaction with only one reactant, that is, a reaction of the type A P where the rate law is rate r = k [A]².

Experiment I : Determination of the effect of concentration of the acid on the reaction between magnesium and acids.

Requirements : 250 cm³ of 0.1 mol dm^-3 H₂SO₄ , Six pieces of 2.0 cm cleaned magnesium ribbon.

Method

Mg(s) + H₂SO₄(aq) → MgSO₄(aq) + H₂(g)

• Into a boiling tube, 10.0 cm3 of water is added and marked with a rubber band.

• Into the same boiling tube, 40.0 cm³ of 0.1 mol dm^-3 H₂SO₄ is added and filled with water brimfully.

• The cleaned magnesium ribbon is fixed as shown in the diagram to the bung, the tube is closed with the bung and turned upside down while switching on the stop watch simultaneously.

• Time taken by the gas to fill up to the level of the rubber band is measured.

• Measurement of time is repeated for different solutions tabulated below, every time
fixing a fresh Mg ribbon.

•Calculate the concentration of each acid solution and plot a graph between [H⁺] and 1/t.

R ∝ [H⁺]ⁿ

Initial rate = Average rate for a small change from the starting point

= Volume of gas produced/Time    = Constant/Time  = k/t

R ∝ 1/t

[H⁺]ⁿ ∝ 1/t

Experiment II : Determination of the effect of concentration on the rate of the reaction between Na₂S₂O₃ and HCl.

Requirements : 0.10 mol dm-3 Na₂S₂O₃ solution. 2.0 mol dm^-3 HCl solution, stop
watch, boiling tubes, measuring cylinders, 50 cm³ beaker.

S₂O₃^2-(aq) + 2H⁺(aq)  →  S(s) + SO₂(g) + H₂O(l)

Method
• Given volume of Na₂S₂O₃ solution as shown in the table is added to a 50 cm³ beaker.

• The beaker containing the Na₂S₂O₃ solution is kept on a white paper marked with a cross. Relevant volume of the HCl solution is added and the time to disappear the cross is measured keeping the eye at a constant height from the beaker.

• The beaker is cleaned and the experiment is repeated mixing the solutions given in the table below.

(i) Determining the relationship between the reaction rate and the thiosulphate ion concentration.
The experiment is done using thiosulphate solutions of different concentrations as given in the table.

R ∝ [S₂O₃^2-(aq)]ⁿ

(ii) Determining the relationship between the reaction rate and the concentration of hydrogen ions.
The experiment is done using acid solutions of different concentrations as given in the
table.

R ∝ [H⁺]ⁿ

In both the above instances, assume that the rate is constant during the period of measurement of time taken to disappear cross and it is equal to the initial rate. Then, Rate = constant / t
In both instances examine how concentration varies with 1/t.

Experiment III : Determination of the effect of concentration on the rate of the reaction between Fe(III) ions and KI.

2Fe³⁺(aq) + 2I^–(aq) → I₂(aq) + 3Fe²⁺(aq)

The amount of I₂ produced can be used to determine the rate of this reaction. The
minimum iodine concentration required to turn starch blue is 1.0×10^-5 mol dm^-3. Since this is very small, measuring time is difficult. Therefore, time taken to appear blue colour should be delayed to measure the time. This can be affected through a faster reaction which converts I₂ to I^–. For this Na₂S₂O₃ can be used.

2S2O₃^2-(aq) + I₂(aq) → S₄O^2-(aq) + 2I^–(aq)

A known amount of Na₂S₂O₃ is added to the medium. The moment in which Na₂S₂O₃ is over, the solution turns blue. The amount of I₂ formed depends on the amount of Na₂S₂O₃ added
Requirements :
0.10 mol dm^-3 KI solution, 0.10 mol dm^-3 FeCl₃ or Fe(NH₄)(SO₄)₂ solution,
0.10 mol dm^-3 Na₂S₂O₃ solution, 0.10 mol dm^-3 H2SO4 solution, stopwatch

Mix the solutions given in the above table as shown here. Measure the time taken to turn the solution blue.

In both instances examine how rate (1/t) varies with concentration.

According to the shape of the graph, order of the reaction (n) can be determined.

Initial rate, instantaneous rate and average rate

Determining the Average Rate from Change in Concentration over a Time Period

We calculate the average rate of a reaction over a time interval by dividing the change in concentration over that time period by the time interval. For the change in concentration of a reactant, the equation, where the brackets mean “concentration of”, is

Determining the Instantaneous Rate from a Plot of Concentration Versus Time

An instantaneous rate is the rate at some instant in time. An instantaneous rate is a differential rate: -d[reactant]/dt or d[product]/dt.

We determine an instantaneous rate at time t:

• by calculating the negative of the slope of the curve of concentration of a reactant versus time at time t.
• by calculating the slope of the curve of concentration of a product versus time at time t.

Determining the Initial Rate from a Plot of Concentration Versus Time

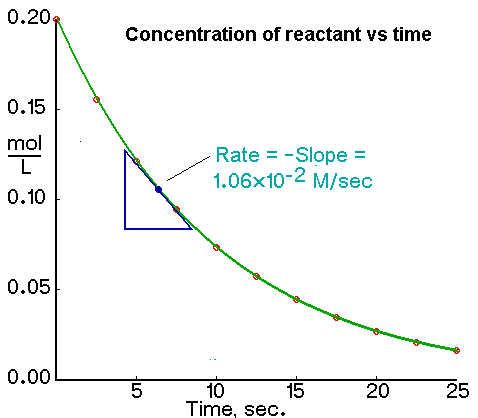
The initial rate of a reaction is the instantaneous rate at the start of the reaction (i.e., when t = 0). The initial rate is equal to the negative of the slope of the curve of reactant concentration versus time at t = 0.

Half life of a reaction

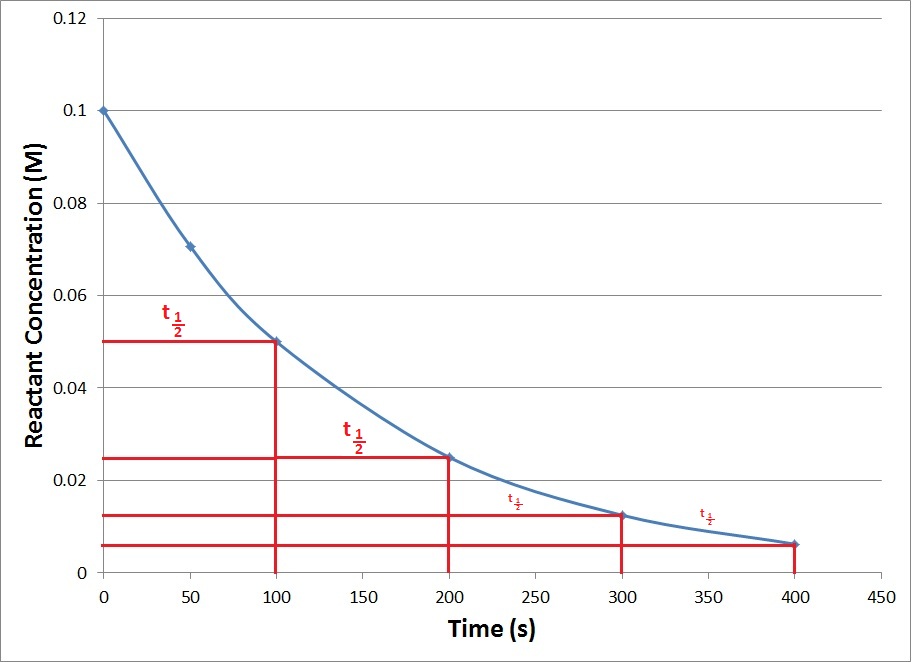
Half life of a reaction is defined as the time required for reducing the concentration of a reactant to half its initial value. It is denoted as t_1/2.

The t_1/2 of a zero order reaction is given as

while for the first order reaction it is given as

Only for the first order reaction t_1/2 is independent of the initial concentration of the reactant. This relation can be used to determine the order of a reaction.