Ionisation of water and Ionic Product of Water ( K_w)

Pure water being a weak electrolyte under goes self ionization to a small extent as follows:

The equilibrium constant for this reaction is:

The concentration of unionized water is taken as constant because the degree on ionization of water is very small. So we can write this equation as:

where K_w is a constant and is known as the ionic product of water whose value is 1.008 x 10^–14 mol² dm^–6 at 298 K. In pure water the concentration of H₃O⁺ and OH^– are equal and so we can write,

[H₃O⁺] = [OH^–]

If, K_w = [H₃O⁺] [OH^–] = 1.008 x 10^-14 mol²  dm^–6 then,

[H₃O⁺] [OH^–] = 1.008 x 10^-14

[H₃O⁺]² = 1.008 x 10^-14

Thus in pure water [H₃O⁺] = [OH^–] = 1.0 x 10^–7 mol  dm^–3 at 298 K

Effect of temperature on K

The value of Kw varies with the change in temperature. The values of [H₃O⁺] and [OH^–] are always equal to each other at all temperatures but the values of K_w are different at different temperatures. The value of K_wincreases with the rise in temperature. This is because increase in temperature will shift the equilibrium in the forward direction producing large concentrations of [H₃O⁺] and [OH^–] ions (Le Chatelier’s principle).

Hence, K_w increases with rise in temperature.

 

It can be concluded that the hydronium and hydroxyl ions are always present in solution whether they are acidic or basic. However their concentrations differ.

 

Dissociation/Ionisation constant of a weak acid (K_a)

An acid HA takes part in the following proton transfer equilibrium in water

HA(aq) + H₂O(l)  ⇌  H3O⁺(aq) + A^–(aq)

 

In this expression, A^– is the conjugate base of the acid.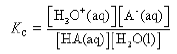

In dilute solution, the concentration of water is constant and the equilibrium can be expressed in terms of the equilibrium constant, K_a.

K_a is the ionisation constant or dissociation constant of the acid.

For acetic acid

Ka is a measure of the acidic strength of the acid.

 

Dissociation/Ionisation constant of a weak base (K_b)

• For a base B in water, the characteristic proton transfer equilibrium is

B(aq) + H₂O(l)   ⇌   BH⁺(aq) + OH^–(aq)

Here, BH⁺ is the conjugate acid. In dilute solutions concentration of H₂O is constant.

Kb is the ionisation or dissociation constant of the base. It is a measure of the strength of the base.

For Ammonia,

NH₃(aq) + H₂O (l)  ⇌  NH₄⁺(aq) + OH^–(aq)

K_b = ( [NH₄⁺] [OH¯] ) / [NH₃]

Kb is a measure of the strength of the base.

 

Relationship between Ka and Kb

Let BH⁺ be the conjugate acid of a base, then the expression for the acidic constant K_a for the conjugate acid:

BH⁺   ⇌  B + H⁺can be written as

          [B] [H+]
  Ka  =  ---------
           [BH+]

          [B] [H+]  [OH-]
      =  --------- ------
           [BH+]    [OH-]

           [B]
      =  -----------  [H+] [OH-]
         [BH+] [OH-]

          1
      =  --- Kw
          Kb

Thus, K_a K_b = K_w

Furthermore,

– log ( K_a) – log (K_b) = -log (K_w)

and at 298 K, we have

p K_a + pK_b = 14

 

• Weak acids and weak bases partially dissociate in water leading to equilibria

• Strong acids like HCl, HNO₃ and strong bases like NaOH completely ionise in water.

Therefore, the H⁺ and OH^– concentration can be directly computed considering the
dissociation.

Ostwald’s law of dilution

For a weak acid 

An acid of the type HA can undergo ionization when dissolved in water as,

If ‘n’ moles of the acid are dissolved in ‘V’ units of volume (litres L) and ‘a‘ is the degree of ionization, then the equilibrium amounts of various species and the concentration in moles per litre in the solution are,

Note that 1 L = 1 dm³

where ‘C’ is the molar concentration of the acid. The ionization constant for the above reaction is given by,

where ‘V’ is the volume of the solution in litres containing one mole of the acid HA. As the degree of ionization increases with-dilution then, the hydronium ion or hydrogen ion concentration is given by,

 

For a weak base

The ionization of a weak base is characterized by the equilibrium,

If ‘n’ moles of the base are dissolved in ‘V’ units of volume (litres L) and a is the degree of ionization, then the equilibrium amounts of various species and the concentration in moles per litre in the solution are,

where ‘C’ is the molar concentration of the base. The ionization constant for the above reaction is given by,

If ‘α‘ is small then 1 – α ≈ 1

Hence, Kb = Cα²

where ‘V’ is the volume of the solution in litres containing one mole of the base MOH. As the degree of ionization increases with dilution then, the hydroxide concentration is given by,

 

pH Value

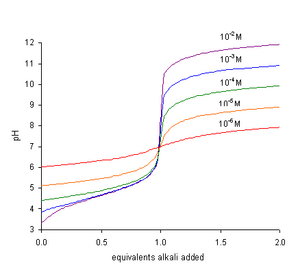
• The concentration of hydronium ions [H₃O⁺] in aqueous solutions is sometimes very small. Hydronium ion concentration of a medium is very important in industrial processes, pollution, acid rain, blood and body chemistry. In many cases its concentration ranges from 10^-14 to 10 mol dm^-3 in aqueous solutions.
• Therefore it is convenient to express the [H₃O⁺] of solutions on logarithmic scale. The negative logarithm of hydronium ions or hydrogen ions concentration is called pH. The ‘p’ in the term pH means power and ‘H⁺‘ stands for hydronium ions or hydrogen ions. The pH is defined mathematically as,
• The negative sign in the definition means that the pH decreases as the hydrogen ion (hydronium ion) concentration increases. A change of one unit in the pH scale corresponds to tenfold change in the hydrogen ion concentration.

 

Calculating the pH of solutions of strong acids

• It is assumed that all strong acids are completely ionised in aqueous solution. The hydronium ion concentration is obtained directly from the concentration of the acid. For monoprotic strong acids [H₃O⁺] is equal to its molar concentration.
Eg. If the concentration of hydrochloric acid solution is 0.1 mol dm^-3.
HCl(aq) + H₂O(l) → H₃O+(aq) + Cl^–(aq)
∴ [H₃O+(aq) ] = 0.1 mol dm^-3
-log₁₀ 0.1 = 1
∴ pH = 1

• Molecules of diprotic strong acids such as sulphuric acid dissociates completely in dilute solutions.
H₂SO₄(aq) + 2H₂O(l) → 2H₃O⁺ (aq) + SO₄^2- (aq)
In 0.1 mol dm^-3 sulphuric acid solution, [H₃O⁺(aq)] = 0.2 mol dm^-3 (assuming complete dissociation)
log₁₀ 0.2 = -0.7
∴ -log₁₀ 0.2 = 0.7
∴ pH = 0.7

Calculating the pH of solutions of strong bases

• Strong bases are also assumed to be completely ionised. The hydroxide ion concentration is therefore easily obtained from the concentration of the base.
eg. Consider 0.3 mol dm^-3 solution of sodium hydroxide.
NaOH (aq) → Na⁺(aq) + OH^–(aq)
[OH^–(aq)] = 0.3 mol dm^-3

• The hydrogen ion concentration of the solution is determined by the ionic product of water. At 298 K the ionic product is 1×10-14 mol² dm^-6. Hydrogen ion concentration at this temperature is given by

 

 

Calculating the pH of solutions of weak acids

• A weak acid does not ionise fully in aqueous solution

By applying equilibrium law,

the degree of dissociation is α and the initial concentration of HA is C

p^H = -log₁₀√(KaC)

Similarly

p^OH = -log₁₀√(KbC)

 

pH of a solution of salt of strong acid and strong base

Let’s take the simplest example absolute; sodium chloride, NaCl. The constituent ions are Na⁺ and Cl^–. The acid-base theory of Bronsted-Lowry has taught us that the more strong the base the weaker it will be its conjugate acid and vice versa, the more strong the acid the weaker will be its conjugate base.

In this case, we have Na⁺, which is the conjugate acid of NaOH, and Cl^–, which is the conjugate base of HCl. NaOH is a strong base, and in the same way HCl is a strong acid. It follows that the Na⁺ acid behavior and Cl^– basic behavior are totally irrelevant.

If none of the two ions interacts with H₂O then we will have no pH changes.

It follows that the pH of an aqueous solution of NaCl is neutral, 7.

The salts derived from strong acid and strong base leave unchanged the pH of a solution.

 

pH of a solution of a salt formed from a weak acid and a strong base

Take for example the sodium acetate, CH₃COONa. And ‘it is including respectively CH₃COO^– and Na⁺. Na⁺ is the conjugate acid of NaOH,and as we saw in the previous example, its contribution to the pH is null. CH₃COO^– instead it is the conjugate base of CH₃COOH, a weak acid. As the conjugate base of a weak acid, it shows a certain affinity towards the proton, and it behaves then as a base:

The acid-base reaction of CH₃COO^– with water is called “hydrolysis.” In this case we are speaking of basic hydrolysis, because the reaction generates an excess of OH^– .Since the reaction generates this excess, the salt of a weak acid and a strong base in water give a pH> 7, ​​therefore alkaline. For the calculation of pH, we can consider the solution of this salt exactly as the solution of just a weak base (in our case CH₃COO^–). We have seen that the formula for calculating generated resulting from a weak base is:

The K_b of the weak base CH₃COO^– can be obtained from K_a of acetic acid as it follows:

The base concentration in this case is the concentration of our salt.

From this considerations the formula for calculating the a salt-strong base weak acid solution:

pOH = -log₁₀√(KwC/Ka) 

 

pH of solution of  salt formed from weak base and strong acid

Take for example the ammonium chloride, NH₄Cl. Its constituent ions are NH₄⁺ and Cl^– .NH₄⁺ is the conjugate acid of NH_3, ammonia, a weak base. It will therefore have a tendency, altough small, to cede that acid hydrogen. Cl^– instead is the conjugate base of HCl, and as we have seen in the examples above its contribution to the pH is practically zero, and then we can overlook it. We can simply consider a solution of this salt as an aqueous solution of the weak acid NH₄⁺ (which will then give an acid pH)

The approximate formula to calculate the pH of a weak acid is the following:

The K_a of the ammonium ion can be easily obtained from the K_b of ammonia. The concentration of acid in the formula, Ca , is therefore in this case the concentration C_s of our salt.

pH of a solution of salt formed from weak acid and weak base

Let’s take for example ammonium acetate, CH₃COONH_4. The constituent ions are CH₃COO^– and NH₄^+. Both of these ions are able to give hydrolysis (as we have seen in the previous examples); CH₃COO^– gives basic hydrolysis, while acid hydrolysis is given by NH₄⁺ .The pH of a salt composed of weak acid and weak base will depend on the strength relationship of the acidic and basic components of the salt. If the base strength and the acid strength are equal the result is a neutral solution. And that’s right the case for example of CH₃COONH₄ .

K_a NH₄⁺  =  K_b CH₃COO^–

If base strength is prevailing on acid strength the salt will give the solution an alkaline pH. And that’s the case for example of NH₄CN.

K_b CN^–  > K_a NH₄⁺

If the prevailing acid strength on the base strength of course the result will be an acid pH.

In any case if we want to exactly calculate the pH of a salt formed by weak acid and weak base (also what we called a neutral solution if we wanted to be accurate, has to be calculated like this because K_a and K_b are always at least slightly different), there is a very simple formula:

In which:

– K_a is the constant of the conjugate acid of the weak base which forms the salt. For example, in the case of CH₃COONH₄ would be the K_a of CH₃COOH.

– K_b is the constant of the conjugate base of the weak acid that constitutes the salt. For example, in the case of CH₃COONH₄ would be the K_bof NH_3.

 

pH Determination

The pH value of a solution can be determined using
• indicators
• indicator papers
• pH meter

 

Theory of indicators

Any acid – base indicator is a weak acid or a weak base. They show one colour below a certain pH value and another colour above a certain pH value.
Consider acid-base indicator as weak acid which can be represented as HIn which takes part in the following equilibrium.
HIn(aq) + H₂O(l)   ⇌  H₃O⁺(aq) + In^–(aq)
Colour I                                                   Colour II

Instead of Ka the equilibrium is described by the constant KIn to show that indicator is used.

KIn = [H₃O⁺(aq)][In^–(aq)]/[HIn(aq)]

-log₁₀KIn = -log₁₀[H₃O⁺(aq)]- -log₁₀[In^–(aq)]- (-log₁₀[HIn(aq)])

pKIn = pH + log₁₀[In^–(aq)]/[HIn(aq)]

 

The HIn and In^– are of two different colours.

The addition of acid to this solution will push the equilibrium to the left and the colour of HIn will become prominent.
Addition of alkali will result in the equilibrium moving to the right since the OH ^–  will remove the H₃O⁺ ion from the equilibrium and the colour of In^– will become prominent.

Colour I displayed at a lower pH may be called ‘lower colour’ and the colour II shown at higher pH can be called the’ higher colour’.

When the pH of the solution becomes equal to pKIn, an intermediate colour of an equimolar mixture of HIn and In^–  is shown.

When the pH range of a particular indicator is equal to pKIn + 1 and pKIn – 1 the colour change occurs over a pH range of about 2 units.

 

• To select the suitable indicator for a particular titration, pH range of the colour change of the indicator should be in the abrupt pH range (vertical portion) that embraces equivalence point of the titration.
• If pH at equilibrium of a titration is equal to the pKIn of an indicator, that indicator fits well for that titration.

Indicator	Color		pKIn	pH range
	Acid	Base
Thymol Blue – 1st change	red	yellow	1.5	1.2 – 2.8
Methyl Orange	red	yellow	3.7	3.2 – 4.4
Bromocresol Green	yellow	blue	4.7	3.8 – 5.4
Methyl Red	yellow	red	5.1	4.8 – 6.0
Bromothymol Blue	yellow	blue	7.0	6.0 – 7.6
Phenol Red	yellow	red	7.9	6.8 – 8.4
Thymol Blue – 2nd change	yellow	blue	8.9	8.0 – 9.6
Phenolphthalein	colorless	magenta	9.4	8.2 – 10.0

 

Calculation of pH value of acid-base reactions at different points and drawing pH curves

• The point at which the reaction completed is called the equivalence point. At the equivalence point of a strong acid- strong base titration,
[H ⁺(aq)] = [ OH ^– (aq)]

• In strong acid –strong base titration neither cation (eg. Na⁺, K⁺) nor the anion (eg. HCl^–,NO₃^–) undergoes hydrolysis at the equivalence point. Therefore, pH at equivalence point is 7.0. Here pH at the equivalence point is determined only by the dissociation of H₂O.

• But in other titrations cations of weak base and anions of weak acid undergo hydrolysis and determine the pH of the resulting solution.

 

Calculation of pH value of acid-base reactions at different points and drawing pH curves

• The term “equivalence point” means that the solutions have been mixed in exactly the right proportions according to the equation.
• The term “end point” is where the indicator changes colour. As you will see on the page about indicators, that isn’t necessarily exactly the same as the equivalence point.

 

Titration curves

1) Strong acid/ strong base titration

We’ll take hydrochloric acid and sodium hydroxide as typical of a strong acid and a strong base.

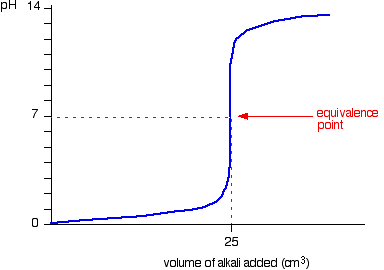
• Titration shows a rapid change in pH from 3 – 11 around its equivalence point. Hence any indicator having pKIn in this range can be used to detect the end point of the titration.
eg. Methyl orange (pKIn = 3.7), Bromothymol blue (pKIn = 7),Phenolpthalene (pKIn = 9.6)
• When concentrations of reactants are low the range in which a rapid change is shown becomes narrow.

 

2) Strong base / weak acid titration

We’ll take ethanoic acid and sodium hydroxide as typical of a weak acid and a strong base.

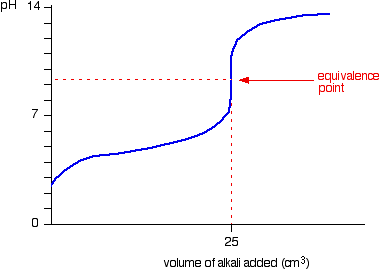
The start of the graph shows a relatively rapid rise in pH but this slows down as a buffer solution containing ethanoic acid and sodium ethanoate is produced. Beyond the equivalence point (when the sodium hydroxide is in excess) the curve is just the same as that end of the HCl – NaOH graph.

For the above titration a rapid change in pH shows around 7.5 to 10. Therefore, the suitable indicator is phenolpthalene. (pKIn = 9.6)

 

3. Strong acid/ weak base titration

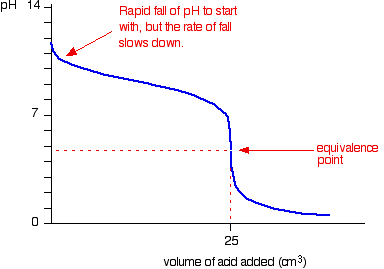
Because you have got a weak base, the beginning of the curve is obviously going to be different. However, once you have got an excess of acid, the curve is essentially the same as before.

At the very beginning of the curve, the pH starts by falling quite quickly as the acid is added, but the curve very soon gets less steep. This is because a buffer solution is being set up – composed of the excess ammonia and the ammonium chloride being formed.

For the above titration a rapid change in pH shows around 3 to 6. Therefore, one of the
suitable indicators is methyl orange.

 

(4) For weak acid – weak base titrations there is no rapid change in pH around the equivalence point. Therefore, it is very difficult to accurately detect the end point by using an indicator.

 

Adding hydrochloric acid to sodium carbonate solution

The overall equation for the reaction between sodium carbonate solution and dilute hydrochloric acid is:

If you had the two solutions of the same concentration, you would have to use twice the volume of hydrochloric acid to reach the equivalence point – because of the 1 : 2 ratio in the equation.

Suppose you start with 25 cm³ of sodium carbonate solution, and that both solutions have the same concentration of 1 mol dm^-3. That means that you would expect the steep drop in the titration curve to come after you had added 50 cm³ of acid.

The actual graph looks like this:

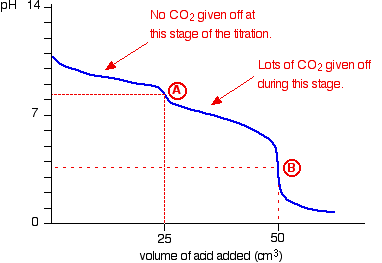
The graph is more complicated than you might think – and curious things happen during the titration.

You expect carbonates to produce carbon dioxide when you add acids to them, but in the early stages of this titration, no carbon dioxide is given off at all.

Then – as soon as you get past the half-way point in the titration – lots of carbon dioxide is suddenly released.

The graph is showing two end points – one at a pH of 8.3 (little more than a point of inflexion), and a second at about pH 3.7. The reaction is obviously happening in two distinct parts.

In the first part, complete at A in the diagram, the sodium carbonate is reacting with the acid to produce sodium hydrogencarbonate:

You can see that the reaction doesn’t produce any carbon dioxide.

In the second part, the sodium hydrogencarbonate produced goes on to react with more acid – giving off lots of CO₂.

That reaction is finished at B on the graph.

It is possible to pick up both of these end points by careful choice of indicator. That is explained on the separate page on indicators.