• Liquid-liquid systems can be classified as
– Totally miscible liquid-liquid systems
e.g. water and ethanol, hexane and heptane, benzene and toluene.
– Partially miscible liquid-liquid systems
e.g. water and butanol, water and ether
– Totally immiscible liquid-liquid systems
e.g. water and tetrachloromethane
In the case of a binary solution composed of totally miscible liquid components A and B, it may be possible that f(A-B) = f(A-A) = f(B-B) where f denotes inter-molecular attractive forces or interactions. Such a solution is called an ideal solution. When the components of an ideal solution are mixed (a) the volume does not change and (b) the enthalpy does not change (and hence there is no observable change in temperature).
• When an ideal solution of A and B evaporates into a vacuum in a closed space, the molecules of both A and B with sufficient kinetic energy to surmount the liquid phase interactions escape from the surface into space above. At the same time, the molecules of A and B in motion in the vapour phase return to the liquid phase. When the rates of these two processes are equal, a dynamic equilibrium sets in. This is testified by the consistency of (a) the total vapour pressure (to which partial pressures of A and B contribute) and (b) the composition of the vapour phase at a constant temperature.
• The composition of the vapour depends on (a) the relative volatilities of A and B (and hence their boiling points) and (b) the relative concentrations of A and B in the solution.
• The higher the volatility and the higher the concentration of a certain component the greater is its tendency to be in the vapour phase and to exert a higher partial pressure.
• In order to find the composition of the vapour of an ideal binary solution quantitatively, let us consider the equilibria existing in a liquid-vapour system.
A(l) ⇌ A(g) ——-(1)
B(l) ⇌ B(g) ——-(2)
If R1 is the rate of moving A from liquid phase to gas phase
R1= k/ [A(l)]
Since [A(l)] is proportional to its mole fraction xA in the liquid phase,
R1= k1 × xA ——-(3)
If R2 is the rate of moving A from gas phase to liquid phase
R2= k” [A(g)]
Since [A(g)], is proportional to its partial pressure PA
R2= k2 × PA ———(4)
At equilibrium R1= R2
According to (3) and (4)
k2PA = k1xA
∴PA = (k1/k2)xA
∴PA = k xA
When xA = 1, PA = P0A
k = P0A
PA= P0A. xA
∴Similarly PB= P0B
Thus, in an ideal solution, the partial pressure of a given component A is equal to the product of the vapour pressure of pure A and the mole fraction of A in the liquid phase at constant temperature. This relationship is called Raoult’s law.
• It is understood that PA < P0A
and PB < P0B
Hence lowering in the vapour pressure of A = P0A– PA = P0A – P0A. xA =P0A (1 – xA ) =P0A. xB
∴ ( P0A– PA )/ P0A = xB
This is an alternate form of Raoults’ law.
• Combining Raoults’ law with Dalton’s law of partial pressures, makes it possible to determine the composition of the vapour phase. If PAB is the total vapour pressure and yA and yB are the mole fractions of A and B in the vapour phase respectively :
PA = PA yA
∴PA = (PA + PB ) yA
∴P0A. xA = (P0A. xA + P0B. xB) yA
• According to Raoult’s law PA= P0A. xA . Since P0A is a constant at constant temperature,the graph of the partial vapour pressure of a component against its
mole fraction in an ideal solution is a straight line.
• Assuming A is more volatile than B(i.e. P0A > P0B and ∴ Tb(A) < Tb(B) the plot of vapour pressures versus mole fractions of an ideal solution will be as follows.
Here PAB is total pressure and PA and PB are vapour pressure of A and B respectively
examples -Hexane and heptane, benzene and toluene, bromoethane and iodoethane, CCl4 and CHCl3,C6H6 and C6D6 (Note : PAB at a given composition is equal to PA + PB).
The boiling boint-composition graph, however, is not a straight line.
• Ideal solutions obey Raoults law. There are solutions which deviate from Raoult’s law. In these f(A-B) ≠ f(A-A) ≠ f(B-B). These are non ideal solutions.
• In some f(A-B) >f(A-A) , f(A-B) >f(B-B) and and the freedom for molecules to escape into the vapour phase is lesser than in the case of an ideal solution.
PA< P0A. xA
PB< P0B. xB
PAB < ( P0A. xA + P0B. xB )
Therefore, the curves in the vapour pressure – composition diagram dips downwards whereas the boiling point – composition curve rises up.
e.g. Propanone and methanol, trichloromethane and propanone, ethanoic acid and water.
These solutions are said to exhibit a negative deviation. When components of such solutions are mixed, temperature increases and volume decreases.
In some others f(A-B) < f(A-A) , f(A-B) < f(B-B) and the molecules tend to escape more freely into the vapour phase than in the case of an ideal solution
PA> P0A. xA
PB> P0B. xB
PAB > ( P0A. xA + P0B. xB )
Thus the curves in the vapour pressure – composition diagram loops upwards. The boiling point curve dips downwards.
e.g. Propanone and carbon disulphide, ethanol and benzene.
These solutions show positive deviations from Raoult’s law.
When solvents of such solutions are mixed, temperature decreases and volume increases.
• Simple distillation can be used to get pure water from a solution of salt in water.
• In addition to a distillation flask, for distillation a condenser is also need
• In simple distillation only one component enters the vapour phase.
Using the phase diagram
. 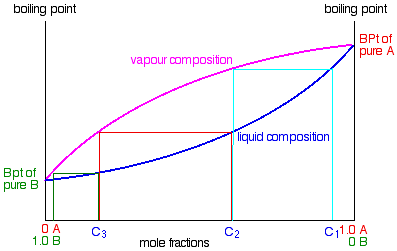
If you boil a liquid mixture C1, you will get a vapour with composition C2, which you can condense to give a liquid of that same composition (the pale blue lines).
If you reboil that liquid C2, it will give a vapour with composition C3. Again you can condense that to give a liquid of the same new composition (the red lines).
Reboiling the liquid C3 will give a vapour still richer in the more volatile component B (the green lines). You can see that if you were to do this once or twice more, you would be able to collect a liquid which was virtually pure B.
The secret of getting the more volatile component from a mixture of liquids is obviously to do a succession of boiling-condensing-reboiling operations.
The apparatus
A typical lab fractional distillation would look like this:
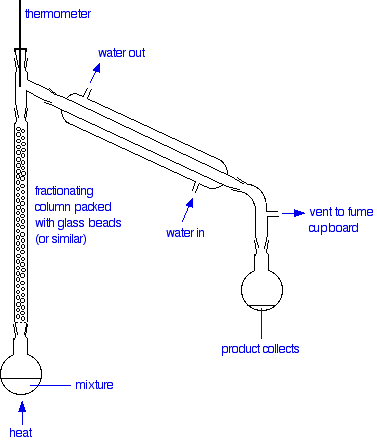
The fractionating column is packed with glass beads (or something similar) to give the maximum possible surface area for vapour to condense on. Some fractionating columns have spikes of glass sticking out from the sides which serve the same purpose.
The mixture is heated at such a rate that the thermometer is at the temperature of the boiling point of the more volatile component. Notice that the thermometer bulb is placed exactly at the outlet from the fractionating column.
Relating what happens in the fractionating column to the phase diagram
Suppose you boil a mixture with composition C1.
The vapour over the top of the boiling liquid will be richer in the more volatile component, and will have the composition C2.
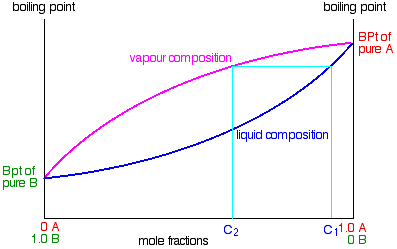
That vapour now starts to travel up the fractionating column. Eventually it will reach a height in the column where the temperature is low enough that it will condense to give a liquid. The composition of that liquid will, of course, still be C2.
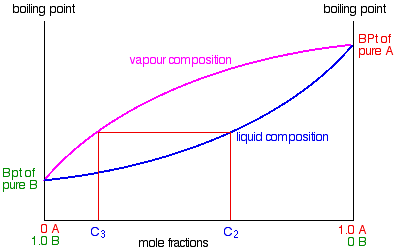
Some of the liquid of composition C2 will boil to give a vapour of composition C3. Let’s concentrate first on that new vapour and think about the unvaporised part of the liquid afterwards.
The vapour
This new vapour will again move further up the fractionating column until it gets to a temperature where it can condense. Then the whole process repeats itself.
Each time the vapour condenses to a liquid, this liquid will start to trickle back down the column where it will be reboiled by up-coming hot vapour. Each time this happens the new vapour will be richer in the more volatile component.
The aim is to balance the temperature of the column so that by the time vapour reaches the top after huge numbers of condensing and reboiling operations, it consists only of the more volatile component – in this case, B.
Whether or not this is possible depends on the difference between the boiling points of the two liquids. The closer they are together, the longer the column has to be.
The liquid
So what about the liquid left behind at each reboiling? Obviously, if the vapour is richer in the more volatile component, the liquid left behind must be getting richer in the other one.
As the condensed liquid trickles down the column constantly being reboiled by up-coming vapour, each reboiling makes it richer and richer in the less volatile component – in this case, A. By the time the liquid drips back into the flask, it will be very rich in A indeed.
So, over time, as B passes out of the top of the column into the condenser, the liquid in the flask will become richer in A. If you are very, very careful over temperature control, eventually you will have separated the mixture into B in the collecting flask and A in the original flask.
