When the rate of formation of a component in a system becomes equal to the rate of loss of it from the system, it is said to be in a steady state. This process can take place in open or closed systems. In a steady state, macroscopic properties do not change.
Examples :
(i) When the rate of inflow of water into a tank is equal to the rate of outflow, the volume of water in the tank remains the same.
(ii) When the ozone layer is considered, the concentration of ozone remains constant due to the following reactions, so it is at the steady state.
O3(g) →UV radiation O(g) + O2(g) → O3(g)
(iii) The concentration of O2 in the atmosphere remains constant due to various processes that release and consume oxygen.
(iv) Think of a candle burning uniformly. Apparently the flame does not change because the rates of entry and exit of materials to and from it are equal. The above systems are not in equilibrium.
Macroscopic properties
The properties experimentally determined or calculated taking a system as a whole are
macroscopic properties. Here no attention is paid to the particles constituting the system.
Consider the following reversible change taking place in a closed system with only A introduced into it at a constant temperature.
A ⇌ B
Initially, the rate of turning A into B is high and the rate of the reverse change is zero. With the formation of B, the rate of turning B into A increases and the rate of A becoming B decreases. At a certain moment, the rates of forward and backward reactions become equal. At this point, the system is in dynamic equilibrium. This can be shown by the graph given below.

• This kind of equilibria are established only if the change is reversible.
• The equilibrium is attained only in closed systems at constant temperature.
• The equilibrium can be approached starting from either end.
• The equilibrium is dynamic, i.e. both forward and reverse processes occur even at equilibrium at the same rate.
• The macroscopic properties of the system do not change at equilibrium.
• Dynamic equilibria are prevalent both in physical and chemical systems.
The following dynamic equilibrium is established between liquid water enclosed in a
closed container and water vapour in the space above it.
H2O(l) ⇌ H2O(g)
Iodine is a solid which sublimes. The following dynamic equilibrium sets in between iodine crystals and iodine vapour above them when some iodine is kept in a closed bottle.
I2(s) ⇌ I2(g)
The existence of an equilibrium between CO gas adsorbed on to charcoal and CO in the
gas phase inside a closed vessel is another example for this type of an equilibrium.
Consider a dilute solution formed by the dissolution of a gas like O2 in water. When this solution is in contact with a gaseous phase containing O2 such as the atmosphere, following equilibrium is established.
O2(solution) ⇌ O2(g)
These occur when a solute is distributed in two immiscible liquids in contact with each other. For instance, I2 dissolves both in water and CCl4. If some water is added to a solution of I2 in CCl4, iodine starts moving into the aqueous layer. With the increase of iodine concentration in the aqueous layer, iodine passes into the CCl4 layer and at a certain stage an equilibrium is established.
I2(H2O) ⇌ I2(CCl4)
These are equilibria encountered in relation to reversible chemical reactions.
N2(g) + 3H2(g) ⇌ 2NH3(g)
NH4Cl(s) ⇌ NH3(g) + HCl(g)
An ionic system should be a chemical system. Such systems contain ions. An equilibrium establishes between chemicals and ions in such systems.
H2O(l) ⇌ H+(aq) + OH–(aq)
AgCl(s) ⇌ Ag+(aq) + Cl–(aq)
CH3COOH(aq) ⇌ CH3COO–(aq) + H+(aq)
When a metal rod is immersed in a solution of its ions initially the metal atoms lose electrons and enter the solution as ions. The electrons reside in the metal. Consequently the metal becomes negatively charged. As the concentration of the metal ions in the solution increases, they capture electrons from the metal surface and become metal atoms. At a certain instant, the rate of ionization of metal atoms becomes equal to the rate of deposition of ions on the metal. At this equilibrium, the potential difference between the negatively charged metal surface and the positively charged metal ions in solution is called the electrode potential of the metal.
eg. Consider a zinc rod sunk in a Zn2+ ion solution.
Zn2+(aq) + 2e ⇌ Zn(s)
According to equilibrium law:
Where K is a constant called equilibrium constant. The symbol [ ] represents the concentrations of respective species at equilibrium.
• K depends only on temperature and is independent of initial and final concentrations of reactants and products. When expressing the equilibrium constant, the following requirements should be fulfilled.
• The relevant balanced equation for the equilibrium reaction should be given (Generally this is written so that the stoichiometric coefficient assume lowest whole numbers).
• The relevant temperature should be given.
• The physical states of the reactants and products should be given.
Attention should be paid to the following also.
• The equilibrium constant does not give any information with regard to the rate of the reaction.
• The value of K does not depend on initial concentrations.
• The value of K depends on temperature.
• By convention, the products are placed in the numerator of the expression.
• Since concentration of a solid or a pure substance is constant, they are incorporated into the equilibrium constant.
• The units of K depends on the expression for K (However, according to thermodynamic treatment, the equilibrium constant is dimensionless).
• The equilibrium constant expressed in terms of concentrations is known as Kc (‘c’ denotes concentration). The units of Kc depends on the stoichiometric equation for which the expression is written.
eg
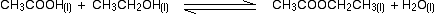
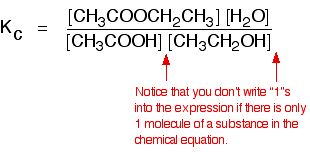
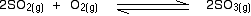
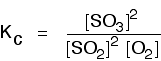
• If the gases in an equilibrium mixture behave ideally,
PV = nRT
n/V = P/RT
c = P/RT
∴At constant temperature, the concentration of a gas is proportional to its pressure. Partial pressure of a gas = mole fraction x total pressure
PG = PT x xG
Partial pressures are therefore proportional to the amount of gases and are used as a measure of concentration of a gas in a gaseous mixture.
• Consider the reaction between nitrogen gas and hydrogen gas, used to produce
ammonia as an example.
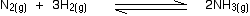
If the partial pressures of the individual gases in the equilibrium mixture are PH2,PN2 and PNH3 respectively then the equilibrium constant in terms of partial pressures Kp is given by expression,
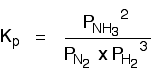
• The partial pressures are treated as exact concentrations so they are raised to the power of the respective stoichiometric coefficient in the equation for the reaction.
• The value Kp describes the position of equilibrium and the concentrations of gases that can co-exist in an equilibrium.
• Reversible thermal dissociation in a closed system gives rise to an equilibrium mixture.
eg-In a closed system dissociation of dinitrogen tetraoxide into nitrogen dioxide
Heterogeneous equilibria
This equilibrium is only established if the calcium carbonate is heated in a closed system, preventing the carbon dioxide from escaping.
![]()
![]()
The only thing in this equilibrium which isn’t a solid is the carbon dioxide. That is all that is left in the equilibrium constant expression.
![]()
In a reaction,
aA + bB ⇌ cC + dD
we can write


Assuming the gaseous components to behave ideally,
PiVi = niRT
or

where (i) is the molar concentration of the species ‘i’.


n = (Number of moles of gaseous products)-(Number of moles of gaseous reactants).
Thus, n is equal to the difference in the number of gaseous moles of products and the number of gaseous moles of reactants. The above equation can be rewritten as
Kp = Kc (RT)Δn

• In a closed vessel at constant temperature, the following equilibrium exits between water and water vapour.
H2O(l) ⇌ H2O(g)
• Applying equilibrium law,
Since [H2O(l)] is a constant, K’ =[H2O(g)]
Since the concentration of a gas is proportional to its pressure at constant temperature, K = P0H2O
Where P0 is the saturated vapour pressure of water at the temperature concerned. Hence, the equilibrium constant of this system can be taken as the saturated vapour pressure of water at the temperature concerned
• It is the equilibrium constant describing the distribution of a solute species between two immiscible solvents.
• Immiscible liquids, if shaken together, mix temporarily but eventually separate into distinct phases with the most dense at the bottom and the least dense at the top. A visible boundary, the meniscus, separates two phases.
• The ratio of the concentration of a solute species that is distributed between two immiscible solvents at a given temperature is a constant.
If you have two immiscible liquids like ether and water, and shake them up in a separating funnel, they obviously form two layers. The ether is less dense than water, and so forms the top layer.
Now suppose you shake up a mixture of ether and water containing a substance which is soluble in both of them. Let’s suppose that the substance, X, is more soluble in ether than it is in water.
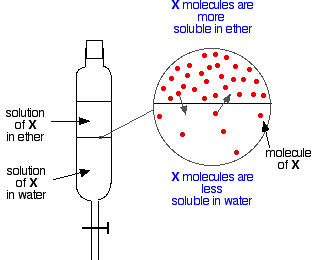
Particles of X will cross the boundary between the two liquid layers, and you will soon get a dynamic equilibrium set up. For every particle which moves into the top layer, one will move back down into the bottom one.
You could write an equation for this:
![]()
![]()
. . . and like any other equilibrium, you can find an equilibrium constant:
![]()
![]()
This equilibrium constant is called the partition coefficient, and is often given the symbol KD.
Like other equilibrium constants, partition coefficients are constant at a constant temperature, but they have some other restrictions as well. They only work properly for fairly dilute solutions, and the solute must be in the same chemical form in both solvents. It mustn’t react, or ionise or associate (join together in dimers, for example)
• The extent of a chemical reaction when equlibrium is established is called the position of equlibrium. This varies from one reaction to another and depends upon the temperatue at which the reaction is performed. The equlibrium constant is a measure of the position of an equlibrium. If equlibrium constant is more than one, then the position of equlibrium is said to lie towards the right.
• The position of equilibrium is not fixed for a reaction but changes as you change the reaction conditions. When a system which is in dynamic equilibrium is disturbed, it tends to respond in such a way as to minimize the disturbance and to restore equilibrium. This is known as Le Chatelier’s principle.
• The following factors change the equilibrium point.
– Concentration
– Pressure
– Temperature
Le Chatelier’s principle can be used to deduce the effect of change of those factors on equilibrium.
• Le Chatelier’s principle is a qualitative treatment of the equilibrium law. Whenever possible attempt must be made to explain facts quantitatively using equilibrium law.
Attention should be paid to the following.
1. Change in concentration of each substance.
2. Increasing the pressure of the system (Decrease in volume here can be considered as an increase in concentration).
3. Introduction of an inert gas or gas that does not affect the reaction, into the system.
4. The influence of temperature on the equilibrium constant is not discussed. Therefore, use Le Chaterlier’s principle to predict the results of changes in temperature takingexothermic/endothermic nature of the reaction.
5. A catalyst does not change the position of the equilibrium.
