Steady flow                                                                                                                                                             All the fluid particles that pass any given point, follow the same path at same speed.                                     In steady flow streamlines never cross each other.

Laminar flow                                                                                                                                                          In laminar flow, the velocities of all the particles on any given streamline are equal.

Turbulent flow                                                                                                                                                          Above a certain critical speed,fluid become turbulent .It is an  irregular flow ,we can’t predict the motion.

Incompressible fluid

In incompressible fluid change in pressure produces no change in density of the fluid.                                     Liquids can be considered incompressible and gases can be considered for small pressure differences.

Viscous force

When two layers of liquid are moving with different velocities they experience tangental forces which tend to retard the faster layer and accelerate the slower layer.These forces are called viscous forces.

Ideal fluid flow means a fluid incompressible,non viscous at streamline flow.

Equation of continuity

If a fluid is undergoing streamline flow then the mass of fluid which enters one end of a tube of flow must be equal to the mass that leaves at the other end during same time.

Example – Equation of Continuity

10 m³/h of water flows through a pipe with 100 mm inside diameter. The pipe is reduced to an inside dimension of 80 mm.

Using equation (2) the velocity in the 100 mm pipe can be calculated

(10 m³/h) (1 / 3600 h/s) = v₁₀₀ (3.14 (0.1 m)² / 4)

or

v₁₀₀ = (10 m³/h) (1 / 3600 h/s) / (3.14 (0.1 m)² / 4)

    = 0.35 m/s

Using equation (2) the velocity in the 80 mm pipe can be calculated

(10 m³/h) (1 / 3600 h/s) = v₈₀ (3.14 (0.08 m)² / 4)

or

v₈₀ = (10 m³/h) (1 / 3600 h/s) / (3.14 (0.08 m)² / 4)

= 0.55 m/s

Energy possessed by a fluid

Fluid Kinetic Energy

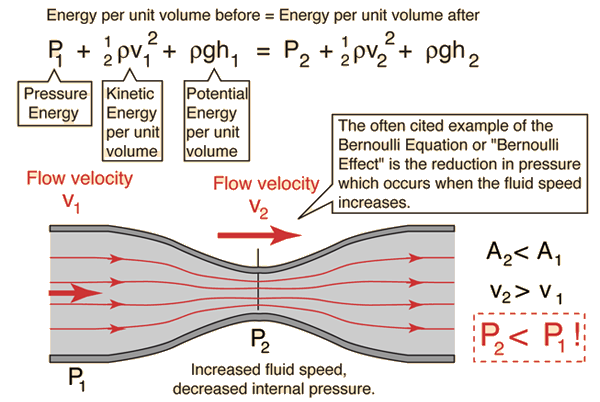
The kinetic energy of a moving fluid is more useful in applications like the Bernoulli equation when it is expressed as kinetic energy per unit volume

Fluid Potential Energy

The potential energy of a moving fluid is more useful in applications like the Bernoulli equation when is expressed as potential energy per unit volume

Pressure as Energy Density

Pressure in a fluid may be considered to be a measure of energy per unit volume or energy density. For a force exerted on a fluid, this can be seen from the definition of pressure:

Bernoulli’s principle

The Bernoulli Equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids.

Applications

• Bernoulli’s principle can be used to calculate the lift force on an airfoil, if the behaviour of the fluid flow in the vicinity of the foil is known. For example, if the air flowing past the top surface of an aircraft wing is moving faster than the air flowing past the bottom surface, then Bernoulli’s principle implies that the pressure on the surfaces of the wing will be lower above than below. This pressure difference results in an upwards lifting force. Whenever the distribution of speed past the top and bottom surfaces of a wing is known, the lift forces can be calculated (to a good approximation) using Bernoulli’s equations established by Bernoulli over a century before the first man-made wings were used for the purpose of flight. Bernoulli’s principle does not explain why the air flows faster past the top of the wing and slower past the underside. See the article on aerodynamic lift for more info.

• The carburettor used in many reciprocating engines contains a venturi to create a region of low pressure to draw fuel into the carburettor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli’s principle; in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.
• An injector on a steam locomotive (or static boiler).
• The pitot tube and static port on an aircraft are used to determine the airspeed of the aircraft.
• The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate, which can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, the continuity equation shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid flow speed. Subsequently, Bernoulli’s principle then shows that there must be a decrease in the pressure in the reduced diameter region. This phenomenon is known as the Venturi effect.

Airfoil

One of the most common everyday applications of Bernoulli’s principle is in air flight. The main way that Bernoulli’s principle works in air flight has to do with the architecture of the wings of the plane. In an airplane wing, the top of the wing is somewhat curved, while the bottom of the wing is totally flat. While in the sky, air travels across both the top and the bottom concurrently. Because both the top part and the bottom part of the plane are designed differently, this allows for the air on the bottom to move slower, which creates more pressure on the bottom, and allows for the air on the top to move faster, which creates less pressure. This is what creates lift, which allows planes to fly. An airplane is also acted upon by a pull of gravity in which opposes the lift, drag and thrust. Thrust is the force that enables the airplane to move forward while drag is air resistance that opposes the thrust force.

Venturi meter