When an object moves in a path where the distance from a fixed to that object is constant.Then its path is a circle and and its motion is called circular motion.

Angular displacement

Angular velocity

In a circular motion ,with time distance changes.At the same time angle also changes.So there is a need to define angular velocity.

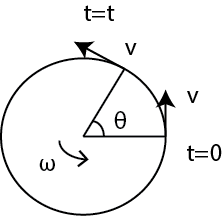Rate of change of angular displacement is called angular velocity

[ω]=T^-1

unit – rads^-1

In uniform circular motion velocity is not uniform because in every point direction changes

In time t, distance traveled= S

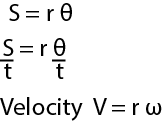
Time period(T)-Time taken for one complete revolution.

Frequency-In unit time number of revolutions take place.

In 1s number of revolutions=f

In 1s angle it makes=2πf

Angular velocity ω=2πf

Centripetal acceleration

In a uniform circular motion acceleration is always directed towards the center.So it is called centripetal acceleration.

Centripetal force

Centripetal force is a force which acts on a body moving in a circular path and is directed towards the center around which the body is moving.

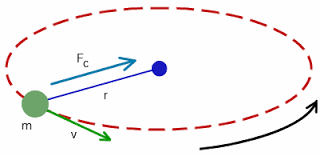  F_centripetal = mrω²

Banked curve

The above image  shows a ball in circular motion on a banked curve. The curve is banked at an angle θ from the horizontal, and the surface of the road is considered to be slippery. The objective is to find what angle the bank must have so the ball does not slide off the road.Intuition tells us that, on a flat curve with no banking at all, the ball will simply slide off the road; while with a very steep banking, the ball will slide to the center unless it travels the curve rapidly.

Apart from any acceleration that might occur in the direction of the path, the lower part of the image above indicates the forces on the ball. There are two forces; one is the force of gravity vertically downward through the center of mass of the ball mg, where m is the mass of the ball and g is the gravitational acceleration ; the second is the upward normal force  exerted by the road perpendicular to the road surface ma_n. The centripetal force demanded by the curved motion is also shown above. This centripetal force is not a third force applied to the ball, but rather must be provided by the net force on the ball resulting from vector addition of the normal force and the force of gravity. The resultant or net force on the ball found by vector addition of the normal force exerted by the road and vertical force due to gravity must equal the centripetal force dictated by the need to travel a circular path. The curved motion is maintained so long as this net force provides the centripetal force requisite to the motion.

The horizontal net force on the ball is the horizontal component of the force from the road, which has magnitude F_h = ma_nsinθ. The vertical component of the force from the road must counteract the gravitational force: F_v = ma_ncosθ = mg, which implies a_n=g / cosθ. Substituting into the above formula for F_h yields a horizontal force to be:

On the other hand, at velocity v on a circular path of radius r, kinematics says that the force needed to turn the ball continuously into the turn is the radially inward centripetal force F_c of magnitude:

Consequently, the ball is in a stable path when the angle of the road is set to satisfy the condition:

or,

As the angle of bank θ approaches 90°, the tangent function approaches infinity, allowing larger values for v²/r. In words, this equation states that for faster speeds the road must be banked more steeply (a larger value for θ), and for sharper turns (smaller r) the road also must be banked more steeply. When the angle θ does not satisfy the above condition, the horizontal component of force exerted by the road does not provide the correct centripetal force, and an additional frictional force tangential to the road surface is called upon to provide the difference. If friction cannot do this , the ball slides to a different radius where the balance can be realized.

In vertical circular motion