The temperature, pressure, volume and the amount (moles) of substance of a gas are the factors that affect the behaviour of a gas.The ideal gas equation can be described as a relationship of the above four variables regarding a gas.

PV = nRT                                        The constant R = 8.314 J K^-1 mol^-1                                                                • Any gas which obeys the above relationship under any given temperature and pressure is referred as an ideal gas.

Derivation of Boyle law from the ideal gas equation PV= nRT

For a fixed mass of gas at constant temperature the product nT is constant. As R is constant                           nRT = k (a constant)

  PV = k

That is the pressure of a fixed mass of gas at constant temperature is inversely proportional to the volume of the gas (Boyle Law).

Derivation of Charles law from the ideal gas equation

Derivation of Avogadro’s law from the ideal gas equation

 

• Molar volume

The molar volume of a gas is the volume of one mole of gas. Molar volume of a gas varies with temperature and pressure. Volume of one mole of a gas at 0 °C and 1 atm is defined as the molar volume of a gas at standard temperature and pressure.

Alternative forms of ideal gas equation

PV = nRT

PV = (w/M)RT

PM = (w/V) RT                                                                                                                                                             PM = dRT                     where d- density

P = (n/V)RT                                                                                                                                                                   P = cRT

 

Assumptions of the molecular kinetic theory of an ideal gas

• Molecules move randomly in straight lines in all directions and at various speeds.

• Gas molecules in random motion collide with each other and with the wall of the container. Such collisions are completely elastic.

• There are no attractions or repulsions between molecules.

• When compared with the distance between molecules, volume of molecules is considered as negligible. • When molecules collide with one another and bounce off the total kinetic energy of the system remains the same.

• The pressure exerted by a gas is the result of collisions of the molecules on the walls of the container.

Molecular kinetic equation is 

P = pressure, V = volume of gas ,     m = mass of a gas particle/molecule   ,                                                       N = number of gas particles/molecules

_                                                                                                                                                                                      c²= mean square speed

 

 

 

The spreading of a certain type of molecules throughout space occupied by another type of molecules is called diffusion.                                                                                                                                                             Example :- When a substance with a scent is kept inside a room, diffusion takes place until the scent is distributed uniformly throughout the room.

Rate of diffusion – solids < liquids < gases

It has been experimentally found that different gases diffuse at different rates. The production of ammonium chloride by the diffusion of ammonia and hydrogen chloride molecules through air can be demonstrated by the following apparatus. From this it is clear that the rate of diffusion of ammonia molecules with a low molecular mass is higher than that of hydrogen chloride molecules.

Factors affecting the rate of diffusion of a gas – molar mass, area, concentration gradient and temperature.

Variation of the mean speed of a gas with temperature is shown by the following Maxwell – Boltzmann curves.

 

 

Compressibility factor

z is the compressibility factor. For ideal gases z = 1. But the fact that this value is not a constant for real gases is revealed by experimental data.

 

The graph of the product PV against P for different gases at the temperature 273 K

• According to this graph it is clear that real gases approach ideal behaviour under conditions of low pressure.

 

The graph of PV/RT against P for a mole of nitrogen at various temperatures.

It is clear from the above graph that at high temperatures the real gases approach ideal behaviour.

Van der Waals equation

 

 

P = Pressure

V = Volume

n = Amount (moles) of substance

R = Universal gas constant

T = Absolute temperature a and b are constants (Van der Waals constants) for real gases

(n²a)/V²  is the correction for pressure drop due to Van der Waals interactions. nb is the correction for the volume of gas molecules.

• The contributions made by the constituent gases towards the total pressure of a mixture of gases is called their partial pressures.

• The pressure that a constituent gas of a mixture of gases would exert if it alone occupies the volume of the container of the mixture is equal to the partial pressure of that gas.

Dalton’s law of partial pressures

In a mixture of gases which do not react with each other the total pressure is equal to the sum of the partial pressures of each of the constituent gases.

• If the partial pressures of individual gases in a mixture of gases A, B and C are PA , PB and PC respectively, total pressure of the mixture Pt = PA + PB + Pc

 

• Avogadro constant (L) is given by the equation                                                                                                                                                                                                                                                                                                  where N = number of particles n = amount of substance Avogadro constant (L) = 6.022 x 10²³ mol ^-1

• Faraday constant (F) Faraday constant is defined as the molar charge of the proton.                                      F = e L              L – Avogadro constant e – Charge of the electron Faraday constant (F) = 96500 C mol^-1

 

• There are various ways in which the composition can be expressed.                                                                    They are; Mass fraction                                                                                                                                                                Volume fraction                                                                                                                                                            Mole fraction                                                                                                                                                                  Mass/volume                                                                                                                                                                Moles /volume

• When the composition is expressed in terms of moles / volume it is called as concentration.

• Composition of a mixture can be expresed as a fraction

Mass fraction

Mass fraction, denoted by ‘w’ is defined as “the ratio of mass of the solute and the total mass of solute and solvent present.”

In a mixture of A and B,

Volume fraction

 

 

 

 

• Composition stated as the number of parts per million of parts (ppm) = fraction x 10⁶

• Composition stated as the number of parts per billion of parts (ppb) = fraction x 10 ⁹

Composition of substances present in very small amounts is commonly expressed in terms of parts per millions (ppm) and parts per billion (ppb).

• Density of water is 1000 g dm^-3 . Density of a dilute aqueous solution can be considered as approximately equals to the density of water. Therefore, mass of 1 dm³ of a solution = 1 kg = 1000 g = 1000000 mg For such instances, mass/ volume ratio can also be expressed in ppm.                                  As a mass fraction, 1 ppm means that 1 000 000 mg of the mixture contains 1 mg of the particular substance.

For dilute solutions, 1 ppm = 1 mg dm^-3 = 1 g cm^-3

 

• Empirical formula : The formula that shows the simplest whole number ratio between the number of atoms in agreement with the composition of a compound is its empirical formula                                               eg. : Empirical formula of benzene is CH

• Molecular formula : The formula that shows the exact number of atoms in a molecule of a compound is its molecular formula.                                                                                                                                                     eg : Molecular formula of benzene is C₆H₆

The ratio between the empirical formula mass and the molecular formula mass of a compound is a whole number

Molecular formula = (Empirical formula) _n

 

 

A chemical equation should be balanced with respect to mass and charges of ions in order to get quantitative information from it.

balancing simple nuclear equation

 

Inspection method

Balancing an equation by balancing the number of atoms of each kind in the reactants and products is called inspection balancing.

Balancing redox equations by checking the changes in oxidation number

One way to balance redox reactions is by keeping track of the electron transfer using the oxidation numbers of each of the atoms. For the oxidation-number-change method, start with the unbalanced skeleton equation. The example below is for the reaction of iron(III) oxide with carbon monoxide. This reaction is one that takes place in a blast furnace during the processing of iron ore into metallic iron

Fe2O3(s)+CO(g)→Fe(s)+CO2(g)

Step 1: Assign oxidation numbers to each of the atoms in the equation and write the numbers above the atom.

                 +3   -2        +2 -2      0        +4 -2                                                                                                                                   Fe2O3(s)+C O(g)→Fe(s)+CO2(g)

Step 2: Identify the atoms that are oxidized and those that are reduced. In the above equation, the carbon atom is being oxidized since its oxidation increases from +2 to +4. The iron atom is being reduced since its oxidation number decreases from +3 to 0.

Step 3: Use a line to connect the atoms that are undergoing a change in oxidation number. On the line, write the oxidation-number change.

The carbon atom’s oxidation number increases by 2, while the iron atom’s oxidation number decreases by 3. As written, the number of electrons lost does not equal the number of electrons gained. In a balanced redox equation, these must be equal. So, the increase in oxidation number of one atom must be made equal to the decrease in oxidation number of the other.

Step 4: Use coefficients to make the total increase in oxidation number equal to the total decrease in oxidation number. In this case, the least common multiple of 2 and 3 is 6. So the oxidation-number increase should be multiplied by 3, while the oxidation-number decrease should be multiplied by 2. The coefficient is also applied to the formulas in the equation. So a 3 is placed in front of the CO and in front of the CO₂. A 2 is placed in front of the Fe on the right side of the equation. The Fe₂O₃ does not require a coefficient because the subscript of 2 after the Fe indicates that there are already two iron atoms.

Step 5: Check the balancing for both atoms and charge. Occasionally, a coefficient may need to be placed in front of a molecular formula that was not involved in the redox process. In the current example, the equation is now balanced.

Fe2O3(s)+3CO(g)→2Fe(s)+3CO2(g)

 

Balancing equations using oxidation / reduction half reactions

Balancing redox reactions is slightly more complex than balancing standard reactions, but still follows a relatively simple set of rules. One major difference is the necessity to know the half-reactions of the involved reactants; a half-reaction table is very useful for this.  Half-reactions are often useful in that two half reactions can be added to get a total net equation. Although the half-reactions must be known to complete a redox reaction, it is often possible to figure them out without having to use a half-reaction table. This is demonstrated in the acidic and basic solution examples. Besides the general rules for neutral conditions, additional rules must be applied for aqueous reactions in acidic or basic conditions.

The method used to balance redox reactions is called the Half Equation Method. In this method, the equation is separated into two half-equations; one for oxidation and one for reduction.

Each equation is balanced by adjusting coefficients and adding H₂O, H⁺, and e^– in this order:

1. Balance elements in the equation other than O and H.
2. Balance the oxygen atoms by adding the appropriate number of water (H₂O) molecules to the opposite side of the equation.
3. Balance the hydrogen atoms (including those added in step 2 to balance the oxygen atom) by adding H⁺ ions to the opposite side of the equation.
4. Add up the charges on each side. Make them equal by adding enough electrons (e^–) to the more positive side. (Rule of thumb: e^– and H⁺ are almost always on the same side.)
5. The e^– on each side must be made equal; if they are not equal, they must be multiplied by appropriate integers (the lowest common multiple) to be made the same.
6. The half-equations are added together, canceling out the electrons to form one balanced equation. Common terms should also be canceled out.

• (If the equation is being balanced in a basic solution, through the addition of one more step, the appropriate number of OH^– must be added to turn the remaining H⁺ into water molecules.)
• The equation can now be checked to make sure that it is balanced.

 

chemical bond –  The electrons in the valence shell of the atom are involved in the formation of bonds.                                    The attraction present between the atoms so as to minimize the energy in a                                                    polyatomic system is called a chemical bond.

Ionic bonds

• The electrostatic attraction between positive and negative ions that are formed when the valence electrons of one atom are given to another atom during the formation of a bond between a pair of atoms with a high difference in electronegativity, is called the ionic bond.

• When sodium chloride in the solid state is considered, the ions are attracted electrostatically and packed in a definite pattern. Therefore, when an ionic compound exists in the solid state, ions do not have the ability for movement. Particles can only vibrate while being in the places where they are situated. Accordingly, an ionic crystal does not conduct electricity.

• When sodium chloride in the liquid state is considered, the ions exist separately. An ionic compound in the molten state conducts electricity because ions have the ability of movement.

Polarization-Polarizing power of a cation and polarizability of an anion

• When an ideal ionic compound is considered, the anion and cation which are its components are regarded as existing in the form of regular solid spheres. But depending on the nature of the cation and the anion which are the constituents of the ionic compound, the cation attracts the electron cloud (polarizing power of the cation) of the anion and at the same time repels the nucleus thus distorting or polarizing the anion and as a result distortion occurs in the electron cloud of the anion (polarizability and tendency to undergo polarization). If the degree of polarization is insignificant the bond remains ionic whereas if it significant electron cloud will be pulled towards the cation resulting in a considerable degree of covalent character.

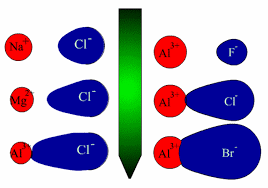⇓ Increase in polarization of the anion . Showing Covalent character to a considerable extent.

 

Cation : If cation is Smaller in size Highly charged or both, polarizing power is high.

Anion : If anion Larger in size Highly charged or both , polarizability is high (tends to distort or polarize).

Examples : In AgF, AgCl, AgBr and AgI the ionic properties vary as follows. AgF > AgCl > AgBr > AgI

When the anion becomes larger the polarizability increases with the resulting increase of                                covalent character. CsI > KI > NaI > LiI

When the cation becomes smaller the polarizing power increases with the resulting increase of covalent character.                                                                                                                                                                MCO3 → MO + CO2                                                                                                                             Breaking up of the group into O^2- and CO2 is influenced by the polarizing power of the M²⁺ ion.

The polarizing power of the cations in Group II varies in the order, Be>Mg>Ca. Therefore the thermal decomposition temperatures of group two carbonates vary in the order BeCO3 < MgCO3 < CaCO3 .

Covalent bonds

• Covalent bonds are formed by keeping the bond pair of electrons common to both the atoms. Covalent bonds are formed by the overlapping of atomic orbitals.

• If the electronegativity difference between two covalently bonded atoms is zero, the bond is referred as a non-polar covalent bond. Other covalent bonds are referred as polar covalent bonds.

• A bond can be formed by the overlapping of an orbital containing lone pair of electrons with the empty orbital of the valance shell of another atom. The bond formed in this way is called the dative bond. There, the species which give the lone pair of electrons is called the donor group (Lewis base) and the species that receives the electrons to form the bond is called the acceptor group (Lewis acid).

Metallic bonds

The electrons in the valence shell of metallic atoms are loosely bonded to the atom. Therefore, there is a tendency for the metallic atoms to release the electrons in valence shell and exist as positive ions. As a result a system is formed in which positive ions are immersed in a sea of electrons which were released from the metal atoms. The positive ions and the sea of electrons get attracted electrostatically to form metallic bonds.

Metals conduct electricity due to the presence of free electrons.

Strong metallic bonds are formed when the size of the metal ion decreases, when the charge of the metal ion increases and when the number of electrons contributing to the metallic bond increases.

When the strength of metallic bond increases melting point of the metal also increases.

 Attractions that exist in covalently bonded molecules or in ionic compounds or in metalic latices are referred as primary interactions.

A structure where the covalent bonds in a covalent molecule or an ion group are represented by Lewis dot symbols, with shared pairs of electrons shown by a short line or a pair of dots (or a pair of dot – cross), and the lone pair of electrons on each atom by pairs of dots or pairs of crosses, is called a Lewis structure. In the Lewis structure only the valence electrons are shown.

Example – Consider H2O molecule.

Lewis dot – cross structure of the molecule of water

 

 

 

 

Lewis structure of the molecule of water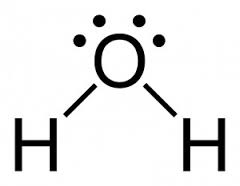

 

 

 

From a Lewis structure information can be obtained about the way that atoms are attached in a molecule, how the number of electrons in the valence shells are distributed and also about the type of the bonds formed. But the Lewis structure does not give information about the shape. By obtaining the number of bond electron pairs and the number of lone pairs situated around the central atom of a molecule from the Lewis structure, the shape of the molecule can be predicted by applying the valence shell electron pair repulsion(VSEPR) theory .

 

 

 

There are occasions where two or more Lewis structures exist for a given same molecule or the ion group which differ from one another only due to differences in the electron arrangement. Such structures that exist for a certain molecule are known as resonance structures. The actual structure of the molecule is not the same as any of these but is a more stable different structure formed by the hybridization of resonance structures. The resonance structures/resonance forms/canonical structures do not have independent existence, but merely drawn for convenience.

Resonance structures for O3

 

 

 

• A formation where the building units are attached to one another in an orderly pattern can be described as a lattice.

•Presence of a formal pattern and the formation from a repetitive basic unit is a common feature of the lattices.

• Various substances with lattice like structures exist in nature. Substances with atoms or molecules or ions arranged in orderly lattice patterns exist.

• Substances with lattice arrangements can be classified according to their building units as follows.               • Homoatomic lattices                                                                                                                                                   • Polar molecular lattices                                                                                                                                             • Heteroatomic lattices                                                                                                                                                 • Ionic lattices                                                                                                                                                                 • Non – polar molecular lattices

• Bonding formed during the formation of the lattice are different, depending on the nature of the building unit of the lattice substance. The nature of the bonding formed during the formation of the lattice affects the physical properties of the lattice.

Homoatomic lattices

Diamond and graphite lattices which are formed from homogeneous atoms are examples for homoatomic lattices.

Lattice arrangement of diamond

Lattice arrangement of graphite

Heteroatomic lattices

• silicon dioxide which is formed from heterogeneous atoms is an example for heteroatomic lattices.

• Homogeneous and heterogeneous atomic lattices are formed by atoms covalently bonding with one another.

• Substances composed of homogeneous and heterogeneous atomic lattices have a high hardness and also higher melting points/ boiling points because such lattices are formed by strong covalent bonds. There is no tendency to go into solution because the covalent bonds present in atomic lattices are very strong.

 

• Electricity is not conducted through atomic lattices as they lack mobile electrons. (Graphite is an exception)

Non-polar molecular lattice

• Iodine crystals which are formed from non polar iodine molecules are examples for non-polarized molecular lattices.

Lattice arrangement of iodine

• Non polar molecular lattices are built by the bonding of non polar molecules to one another by attractive forces formed between induced dipoles.

• the substances with non polar molecular lattices consisting of molecules bonded to one another by weak Van der Waals forces have a low hardness and their melting points/ boiling points are also low relative to substances formed by other lattices.

• the substances formed by non polar molecular lattices dissolve in non polar solvents because they consist of non polar molecules and they do not conduct electricity as they do not possess mobile electrons.

Polar molecular lattice

• Ice which is formed from polar molecules is an example for polar molecular lattice.

• polar molecular lattices are formed by the bonding together of polar molecules to one another by attractive forces developed between permanent dipoles.

• Substances formed by polar molecular lattices show a high tendency to dissolve in polar solvents but do not conduct electricity due to the lack of mobile electrons

• Substances formed by polar molecular lattices consisting of molecules bonded by permanent dipole – permanent dipole attractive forces (or hydrogen bonds) have a high hardness and also higher melting points / boiling points compared to substances formed by non polar molecular lattices.

Ionic lattice •

Sodium chloride which consists of sodium ions and chloride ions is an example for ionic lattice.

• Ionic lattices are formed by the bonding together of ions by strong electrostatic attractions developed between positively charged and negatively charged ions.

• Substances formed by ionic lattices bonded by strong electrostatic attractions show higher melting points/boiling points and also a high hardness.

• The substances with ionic lattices show a tendency to dissolve in polar solvents.

• The substances consisting of ionic lattices do not conduct electricity in the solid state due to the lack of mobile electrons or mobile ions. The substances with ionic lattices conduct electricity in the molten state or in solution because of the presence of mobile ions.