Blog - Page 21 of 55 - Learning & Education Portal

Freefall

A free fall is a downward motion without any initial force or velocity. Our earth has the inherent property of attracting items towards it. Hence a free fall is a natural phenomenon on earth for any object at any height without any support.

Free Fall Speed

An object in motion is governed by two parameters, the velocity and the acceleration. The same concept also applies to free fall. It is too obvious to conclude that an object under free fall has ‘only one’ direction, invariably, vertical downwards. Hence in cases of free fall the velocity can be called in its scalar terms as ‘Free Fall Speed’.

Now we observe that in a free fall, the speed is not uniform. You might have observed that two stones dropped from different heights hit the ground with different velocities. The higher the height, greater is the speed of an object when it reaches the ground. It means that there is some acceleration is imparted on objects under free fall and the same is defined as ‘free fall acceleration’.

Free Fall Acceleration

As per Newton’s second law a force is needed to change the state of rest of any object and hence the law applies to free fall of objects. The action of ‘free fall’ takes place, as we mentioned already, due to an attraction force or gravitation force. When this force is exerted on the object, it is subjected to an acceleration called ‘Free Fall Acceleration’.

This free fall acceleration is constant but naturally the free fall speed is a variable quantity, varies with the time or distance of motion.

In cases of free fall, the distance is better referred as height as the direction is invariably vertical. The free fall acceleration is well known as ‘acceleration due to gravity’. For all practical purposes it is considered as constant at all places of earth and is denoted by the letter ‘g’.

A free fall occurs for an object only due to free fall acceleration and hence its parameters of motion are independent of its mass, when you ignore the air resistance. Normally, the air resistance is very low except in cases of objects with large areas and hence it is a safe bet to ignore that. But at the same time one must realize that the force acquired by an object under free fall is certainly proportional to the mass of the object. In fact such force of the object is nothing but the Net Weight of the object and also its momentum as it hits the ground (mass times the final velocity) depends on the mass of the object.

Let us derive the three important free fall equations considering the free fall without air resistance. Let us assume ‘v’ is the final velocity, ‘h’ is the height and ‘t’ is the time related to a free fall. Obviously the initial velocity for a free fall is 0 and the acceleration in this case is ‘g’.

The final velocity is generally defined as the sum of the initial velocity and the product of acceleration and time.

Therefore, for a free fall,

v = 0 + gt

v = gt ………(1)

The second free fall equation is derived as follows :

The distance covered by an object in any motion is the product of average velocity and time.

Therefore, for a free fall,

h = ½(v + 0)(t) = ½ vt = ½ gt $\times$ t

h = ½gt² ……….(2)

Let us eliminate ‘t’ from these two equations to arrive at the third free fall equation,

v2 = 2gh ……….(3)

Projectile motion

Projectile motion is an example of curved motion with constant acceleration. It is two dimensional motion of a particle thrown obliquely into the air.

Consider the motion and path followed by the ball when it moves in the curved path. We will make two assumptions here:

a) First assumption is that the free fall acceleration (g) remains constant and does not change its value during the motion of the ball.

b) Resistance offered by the ball is negligible.

If we consider the motion and the assumptions stated above, we will find that :

The path of the projectile (ball here) is always a parabola.
The path followed by the projectile is termed as the “trajectory of the projectile“.
Projectile feels only one force while in motion, which is the force of gravity.

Projectile

Projectile Motion Equation

Projectile motion is a two dimensional concept and it follows the two dimensional kinematics. A projectile has both the horizontal and the vertical components of motion.

Projectile motion can be stated as the:

y = $\frac{1}{2}$ (at²) + v₀ t + y₀

Where,
y = height
t = time
a = acceleration of the projectile because of gravity
V₀ = Initial velocity of the projectile
Y₀ = Initial height of the projectile

Horizontal Component of the Velocity : Whenever the projectile is thrown or follows the trajectory, the horizontal component of the velocity does not changes and the displacements covered by the horizontal components of the velocity are uniform. In other words, final horizontal velocity component is equal to the initial velocity component.

Now the point here to note is that when the projectile follows the trajectory, gravity force does not affect or does not make any change in the horizontal velocity component of the velocity.

Vertical Component of the Velocity : Vertical component of the velocity does not remain constant during the projectile motion. Gravity force acts on it and changes the vertical component of the velocity of the projectile. The displacements covered by the vertical component of the velocity are not uniform.

For the vertical component of the velocity during the projectile motion, change in both the magnitude and direction takes place. If the projectile is moving in the upward direction, then the vertical component of the velocity is in the upward direction and decrease in its magnitude takes place.

On the other hand, when the projectile moves in the downward direction, the direction of the vertical components of the velocity is in the downward direction and increase in the magnitude takes place.

Range Equation for Projectile Motion

Equations involving Vertical Motion	Equations involving Horizontal Motion	Explanation of Symbols used

V_(iy) = V_i sin $θ$	V_(ix) = V_icos $θ$	V_i= Magnitude of Initial Velocity V_(iy) = Y component of Initial Velocity V_(ix) = X component of Initial Velocity
V_(fy) = V_(iy) + a_yt	V_(fx) = V_(ix)	V_fy = Y component of Velocity at time ‘t’ V_fx= X component of Velocity at time ‘t’ (note that the X component remains constant) a_y= acceleration in vertical direction, which in the case of projectile motion would be -9.8 m/s²
Y_f – Y_i = V_(iy)t + ½a_yt²	X_f – X_i = V_(ix)t	Y_i = Initial Y co-ordinate of Projectile Y_f = Y co-ordinate of Projectile at time ‘t’ X_i = Initial X co-ordinate of Projectile X_f = X co-ordinate of Projectile at time ‘t’
(V_fy)² = (V_(iy))² + 2a_y(Y_f– Y_i)		Symbols already described above
Y_f – Y_i=t. $\frac{(V_{(i y)} + V_{(f y)})}{2}$		Symbols already described above

Maximum Projectile Range : Expression

Now, lets look at the expression for projectile range using the above formula, Let the projectile start at (0, Yi) co-ordinates with a speed of Vi = v, and angle $θ$ with the horizontal surface. After some time t, it strikes the ground at a distance of Xf. The value of Xf gives the range of the projectile

The figure given below aids the visualization of the motion :

Projectile Range

In this figure, the range of the projectile is given by the formula,

d = $X_{f}$ = $(\frac{(V c o s θ)}{g})$ $(V s i n θ + \sqrt{((V s i n θ)^{2} + 2 g Y_{i})})$

Using the above equation one can make a graph of `theta` versus `d` for different `theta`, and see where the value of `d` maximizes. This will be the value of maximum projectile range. Moreover, this equation reduces to a very simple form when the projectile starts form ground level, that is when $Y_{i}$ = 0.

The equation then becomes :

d =

X_{f}

= $\frac{(2 V^{2} c o s θ s i n θ)}{g}$

d =

X_{f}

= $\frac{(V^{2} s i n (2 θ))}{g}$

Using the above equation we can very easily find the expression for maximum projectile range in this simple situation. We know that the maximum value of sin 2 $θ$ is 1.

Therefore, the maximum range of the projectile is
d = $X_{f}$ = $\frac{V^{2}}{g}$

Also, the value of 2 $θ$ for which sin 2 $θ$ = 1 is $90^{\circ}$ . Therefore, the value of $θ$ = 90/2 = $45^{\circ}$

Horizontal Projectile Motion

This is a type of Projectile motion in which projectile does not follow path in the upward direction or it does not have upward trajectory and the initial velocity of the projectile is also zero. This type of projectile motion is called horizontal projectile motion. This motion generally occurs when the projectile is shot straight without forming any angle with the horizontal surface and the projectile falls downward until it hits the ground.

Exemplary Horizontal Projectile motion is shown in the figure below.

As shown in the figure below, the initial component of the vertical components of the velocity is zero. Horizontal velocity component of the projectile remains constant as the gravity does not affect it. Direction of the vertical component of the velocity is in downward direction during the trajectory. The magnitude of the vertical component of the velocity increases as the projectile moves downward, the force of gravity acts on it, results in acceleration of the projectile.

The figure above illustrates a body thrown horizontally from a point O with a velocity The point O is at a certain height above the ground. Let x and y be the horizontal and vertical distances covered by the projectile, respectively, in time t. Therefore, at time t, the projectile is at p.

In order to calculate x, let us consider the horizontal motion, which is uniform motion. This is because the only force acting on the projectile is the force of gravity. This force acts vertically downwards and hence the horizontal component in zero. Therefore, the equations of motion of the projectile for the horizontal direction is just the equation of uniform motion in a straight line.

$∴$ x = vt —————— (i)

In order to calculate y, the vertical motion of the projectile is considered. Since the vertical motion is controlled by the force of gravity, it is an accelerated motion. The initial velocity, v_y (0), in the vertically downward direction is zero. Since the Y-axis in the figure above is taken downwards, the downward direction is regarded as the positive direction. So, the acceleration of the projectile is + g.

$∴$ from the equation
y(t) = V_y(0)t + ½ a_y t²
We have y(t) = ½ gt² ————-(2)

Here v_y (0) is taken as zero because both distance and time are being measured from the origin O.

From equation (1)
t = $\frac{x}{v}$

Substituting for t from the above equation in equation (2) we have,

y(t) = ½g ${(\frac{x}{v})}^{2}$ = ( $\frac{g}{2 v^{2}}$ )x²

$∴$ y = kx² Where k = $\frac{g}{2 v^{2}}$ ……………..(3)

is a constant for a projectile projected upwards with a definite velocity v and at a place with a definite value of ‘g’.

Equation (3) is a second-degree equation in x, a first-degree equation in y and is the equation of a parabola. Therefore, a body thrown horizontally from a certain height above the ground follows a parabolic trajectory till it hits the ground.

Resultant Velocity of a Horizontal Projectile:

In this section, let us calculate the resultant velocity of the projectile $\vec{V}$ , at any point p on the trajectory, in an interval of time t. V_xand V_y are the horizontal and vertical components of $\vec{V}$ as illustrated in the figure below.

Since, the horizontal motion of the projectile is uniform, ${\vec{V}}_{x}$ = $\vec{V}$

However, the motion in the vertical direction is an acceleration one.

$∴$ V_y(t) = V_y (0) + a_y t

Since O is considered to be the origin, V_y (0) = 0

$∴$ V_v (t) = gt
$∴$ The magnitude of the resultant velocity $\vec{V}$ is given by,

| $\vec{V}$ | = V =√ ( $\sqrt{V_{x}^{2} + V_{y}^{2}}$

$∴$ V = √( $\sqrt{V^{2} + g^{2} t^{2}}$

The direction is given by tan $β$ = $\frac{V_{y}}{V_{x}}$ = $\frac{g t}{V}$

$∴$ $β$ = tan^-1 $\frac{g t}{V}$

Motion -The change of position of a body with time is called motion.

It was Galileo who first realized that motion of a body is independent of its mass, it is the change of state of motion or state of rest.

Inertia

A body is said to possess a property called inertia The inertia of a body is measured by its reluctance to change its state of motion or state of rest. Examples

One’s body movement to the side when a car makes a sharp turn.
Tightening of seat belts in a car when it stops quickly.

Newton’s first law

A body continues its state of rest or moves with uniform velocity unless acted on by some external force.

Linear momentum

Linear momentum is a vector quantity defined as the product of an object’s mass m and its velocity v. Linear momentum is denoted by the letter p .

Note that a body’s momentum is always in the same direction as its velocity vector. The units of momentum are kg m/s.

p=mv

Newton’s second law

The rate of change of momentum of a body is directly proportional to the external force acting on the body and change in momentum takes place in the direction of force.

Newton’s third law

Whenever an object exerts a force on another object,the second object exerts an equal and opposite force on the first.These are called action, reaction. For every action there is always an equal and opposite reaction.

Image result for newton's third law

Note

Forces always appear in pair.
The line of force is always in the same line.
Forces are of same kind.
Forces act on different bodies.

Friction

Friction is the force resisting the relative motion.It comes to existence at the common boundary of two bodies in contact when one of them either moves or tends to move relative to other. Friction acts tangental to the surface and it is directed such that it opposes relative motion.

The surface of a body is never perfectly smooth, little prominences and hollows are always present.When two body is in contact the prominences of one are interlocked with hollows of other.In the relative motion of the bodies these little prominences are deformed and give rise to frictional forces.

Sliding friction

When a body slides over another body , the force that opposes relative motion is called sliding friction.

Specific examples of sliding friction include:

Rubbing both hands together to create heat
A sled sliding across snow or ice
A person sliding down a slide is an example of sliding friction

Rolling friction

When a round object rolls over some surface then rolling friction comes into play.Rolling friction is much smaller than sliding friction.

Examples of Rolling Friction

A car will eventually come to a stop if just allowed to roll as the friction between the road surface and the wheels causes friction that causes the vehicle to stop.
Bike wheels that are thicker will lessen the potential speed of the bike because there is a greater wheel surface to create friction against the surface which will slow the bike.
Heavy duty trucks get greater gas mileage when tread begins to wear on the tires because there is less rolling friction, allowing the truck to move more quickly with less resistance.
A skateboard set on a slight decline will eventually stop itself because of the resistance caused by the friction between the wheels and the surface.

Kinetic friction

When two bodies that are in contact with each other and move rubbing the surfaces that are in contact, the friction existing between them is called kinetic friction. The direction of the force is such that the relative slipping is opposed by the retarding force .

Magnitude of Kinetic Friction
Fk = μk R
Where,
Fk = magnitude of kinetic friction
R = Normal reaction
μk = coefficient of kinetic friction

Note-The coefficient of friction does not depend upon the speed of the sliding bodies. If the surfaces are smooth then it will be small, and it will be large if the surface is rough

Static Friction

The opposing force which comes into play when an object does not move over another object, even when the force is applied to make it move is called Static Friction. Static friction prevents objects from sliding or rolling over each other.
For example, when we push a heavy object, because of the friction the object is unable to move through the surface. Then we apply some force on the object. Once it moves through the surface, it is very easy to move further.
When we were unable to move the object, it was static friction. When it was moving we were overcoming the kinetic friction, which is found to be less than static friction.

Fs = μs R
where,
μ is is the Coefficient of Static friction
R is the Normal reaction

Static friction is greater in magnitude than kinetic friction in any situation.

Relationship between limiting frictional force and normal reaction

Limiting frictional force between two given surfaces depend on the normal reaction between them.To investigate relationship do an experiment with known masses placed on the block.

Initially without mass(m) , apply the force(F) and increase the force until the block in the verge of moving.At that moment take the reading of spring balance.
Now add the known mass(m) to the block and find the force(F) when the block is in the verge of moving.
Do the practical using atleast six different masses(m).

A body is said to perform a pure rotational motion if every particle in the body moves in a circular path such that the centers of all those circles lie on a single straight line called as the axis of rotation.

Angular acceleration

When an object rotates its angular velocity changes with time.Angular acceleration is defined as rate of change of angular velocity.

Image result for angular acceleration formula

[α]=T^-2 Unit – rads^-2

The translational acceleration of a point on the object rotating is given by

a_T=rα

where r is the radius or distance from the axis of rotation. This is also the tangential component of acceleration: it is tangential to the direction of motion of the point.

When the angular acceleration is constant, the five quantities angular displacement $\theta$ , initial angular velocity $\omega _{i}$ , final angular velocity $\omega _{f}$ , angular acceleration $\alpha$ , and time $t$ can be related by four equations of kinematics:

\omega _{f}=\omega _{i}+\alpha t\;\!

\theta =\omega _{i}t+{\begin{matrix}{\frac {1}{2}}\end{matrix}}\alpha t^{2}

\omega _{f}^{2}=\omega _{i}^{2}+2\alpha \theta

\theta ={\tfrac {1}{2}}\left(\omega _{f}+\omega _{i}\right)t

Moment of inertia

The moment of inertia of an object is a measure of the object’s resistance to changes to its rotation. The moment of inertia is measured in kg m². It depends on the object’s mass: increasing the mass of an object increases the moment of inertia. It also depends on the distribution of the mass: distributing the mass further from the centre of rotation increases the moment of inertia by a greater degree.

For a single particle of mass m a distance r from the axis of rotation, the moment of inertia is given by I=mr²

Torque

Torque ${\boldsymbol {\tau }}$ is the twisting effect of a force F applied to a rotating object which is at position r from its axis of rotation.

{\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} ,

A net torque acting upon an object will produce an angular acceleration of the object according to

{\boldsymbol {\tau }}=I{\boldsymbol {\alpha }},

just as F = ma in linear dynamics.

The work done by a torque acting on an object equals the magnitude of the torque times the angle through which the torque is applied

W=\tau \theta .\!

The power of a torque is equal to the work done by the torque per unit time

P=\tau \omega .\!

Angular momentum

The angular momentum L is a measure of the difficulty of bringing a rotating object to rest. It is given by

L = mv×r

Angular momentum is related to angular velocity by

{\mathbf {L}}=I{\boldsymbol {\omega }},

just as p = m v in linear dynamics.

The greater the angular momentum of the spinning object such as a top, the greater its tendency to continue to spin.

The Angular Momentum of a rotating body is proportional to its mass and to how rapidly it is turning. In addition the angular momentum depends on how the mass is distributed relative to the axis of rotation: the further away the mass is located from the axis of rotation, the greater the angular momentum . A flat disk such as a record turntable has less angular momentum than a hollow cylinder of the same mass and velocity of rotation.

Like linear momentum, angular momentum is vector quantity, and its conservation implies that the direction of the spin axis tends to remain unchanged. For this reason the spinning top remains upright whereas a stationary one falls over immediately.

Torque and angular momentum are related according to

{\boldsymbol {\tau }}={\frac {d{\mathbf {L}}}{dt}},

just as F = dp/dt in linear dynamics

Law of conservation of angular momentum

If there is no external torque acting on a system the angular momentum remains unchanged.

L=Iω=constant

Rotational kinetic energy

When an object rotates about an axis every particle in that body moves in a circle then rotational kinetic energy is the sum of total kinetic energy of particle.

Rotational kinetic energy = ½Iω²

When an object moves in a path where the distance from a fixed to that object is constant.Then its path is a circle and and its motion is called circular motion.

Angular displacement

Angular velocity

In a circular motion ,with time distance changes.At the same time angle also changes.So there is a need to define angular velocity.

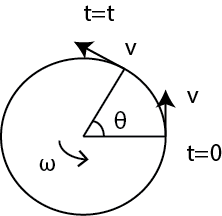Rate of change of angular displacement is called angular velocity

[ω]=T^-1

unit – rads^-1

In uniform circular motion velocity is not uniform because in every point direction changes

In time t, distance traveled= S

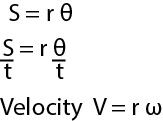
Time period(T)-Time taken for one complete revolution.

Frequency-In unit time number of revolutions take place.

In 1s number of revolutions=f

In 1s angle it makes=2πf

Angular velocity ω=2πf

Centripetal acceleration

In a uniform circular motion acceleration is always directed towards the center.So it is called centripetal acceleration.

Centripetal force

Centripetal force is a force which acts on a body moving in a circular path and is directed towards the center around which the body is moving.

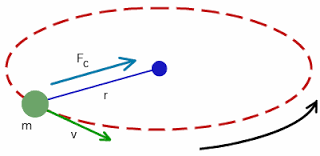F_centripetal = mrω²

Banked curve

The above image shows a ball in circular motion on a banked curve. The curve is banked at an angle θ from the horizontal, and the surface of the road is considered to be slippery. The objective is to find what angle the bank must have so the ball does not slide off the road.Intuition tells us that, on a flat curve with no banking at all, the ball will simply slide off the road; while with a very steep banking, the ball will slide to the center unless it travels the curve rapidly.

Apart from any acceleration that might occur in the direction of the path, the lower part of the image above indicates the forces on the ball. There are two forces; one is the force of gravity vertically downward through the center of mass of the ball mg, where m is the mass of the ball and g is the gravitational acceleration ; the second is the upward normal force exerted by the road perpendicular to the road surface ma_n. The centripetal force demanded by the curved motion is also shown above. This centripetal force is not a third force applied to the ball, but rather must be provided by the net force on the ball resulting from vector addition of the normal force and the force of gravity. The resultant or net force on the ball found by vector addition of the normal force exerted by the road and vertical force due to gravity must equal the centripetal force dictated by the need to travel a circular path. The curved motion is maintained so long as this net force provides the centripetal force requisite to the motion.

The horizontal net force on the ball is the horizontal component of the force from the road, which has magnitude F_h = ma_nsinθ. The vertical component of the force from the road must counteract the gravitational force: F_v = ma_ncosθ = mg, which implies a_n=g / cosθ. Substituting into the above formula for F_h yields a horizontal force to be:

|\mathbf{F}_\mathrm{h}| = m |\mathbf{g}| \frac { \mathrm{sin}\ \theta}{ \mathrm {cos}\ \theta} = m|\mathbf{g}| \mathrm{tan}\ \theta \ .

On the other hand, at velocity v on a circular path of radius r, kinematics says that the force needed to turn the ball continuously into the turn is the radially inward centripetal force F_c of magnitude:

|\mathbf{F}_\mathrm{c}| = m |\mathbf{a}_\mathrm{c}| = \frac{m|\mathbf{v}|^2}{r} \ .

Consequently, the ball is in a stable path when the angle of the road is set to satisfy the condition:

m |\mathbf{g}| \mathrm{tan}\ \theta = \frac{m|\mathbf{v}|^2}{r} \ ,

or,

\mathrm{tan}\ \theta = \frac {|\mathbf{v}|^2} {|\mathbf{g}|r} \ .

As the angle of bank θ approaches 90°, the tangent function approaches infinity, allowing larger values for v²/r. In words, this equation states that for faster speeds the road must be banked more steeply (a larger value for θ), and for sharper turns (smaller r) the road also must be banked more steeply. When the angle θ does not satisfy the above condition, the horizontal component of force exerted by the road does not provide the correct centripetal force, and an additional frictional force tangential to the road surface is called upon to provide the difference. If friction cannot do this , the ball slides to a different radius where the balance can be realized.

In vertical circular motion

Work

The word work is used only in those cases where there is a force and a displacement occurs in the direction of force.

Work done = Force acting on the body × Distance moved in the direction of force

W = F × S

[W] = ML²T^-2

Unit – kgm²s^-2 = joule

1 J – 1 joule is the work done by a force of 1N acting through a distance of 1m in the direction of force.

Power

Power is the rate of doing work.

[P]=ML²T^-3

Unit – kgm² t^-3 =Js^-1 Watts

1Watt – Capable of doing work at the rate of 1Js^-1 is said to possess a power of 1W

t=0 t=t

Work done by applied force W=F×S

Work done by applied force in unit time = F×S/t

Power=F×V

Energy

Ability to do work is called energy.

Kinetic energy

An object has kinectic energy due to its motion.

Kinetic Energy = ½mv²

Gravitational potential energy

Gravitational potential energy is a energy due to the position of the object.

Gravitational potential energy= mgh

Elastic potential energy

Elastic potential energy is Potential energy stored as a result of deformation of an elastic object, such as the stretching of a spring. It is equal to the work done to stretch the spring, which depends upon the spring constant k as well as the distance stretched. According to Hooke’s law, the forcerequired to stretch the spring will be directly proportional to the amount of stretch.

F = -kx

x- extension k-spring constant

Elastic potential energy=½kx² =work done =area of the triangle

Conservation of mechanical energy

Mechanical energy is the sum of the potential and kinetic energies in a system. The principle of the conservation of mechanical energy states that the total mechanical energy in a system (i.e., the sum of the potential plus kinetic energies) remains constant as long as the only forces acting are conservative forces.

Hydrostatics is the branch of fluid mechanics that studies incompressible fluids at rest.

Density

The density of a substance is its mass per unit volume.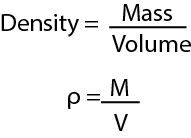

Relative density

the ratio of the density of a substance to the density of a standard, usually water for a liquid.

Pressure in a static fluid When a fluid is at rest , a force only acts at right angles.This is because a fluid cannot sustain a tangental force .When a fluid at rest forces simply act normal to the surface .

p={\frac {F}{A}}

where $p$ is the pressure, $F$ is the normal force, $A$ is the area of the surface on contact.

Pressure is a scalar quantity ,it has no fixed directions.The direction of the force exerted by the liquid is decided by the orientation of area present to the liquid.

Expression for fluid pressure

If we consider atmospheric pressure , say it’s P_o , then the pressure at depth h is given by P = P_o + hρg

In a static liquid, pressures at same level in a same liquid are equal.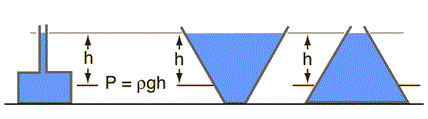

Pressure of atmosphere

Our Earth is surrounded by air upto a considerable height.This envelope of air surrounding the Earth is called atmosphere.Since air has weight, a column of air is capable of exerting pressure.It is first measured by Toricelli.

Image result for simple barometer Atmospheric pressure P_o = hρg

1 atm=1.014 bar= 760 mmHg 1 torr = 1mmHg

Manometer Manometer consist of U tube, it is used to find the difference in pressures between the gas enclosed in a vessel and atmospheric pressure.

Pressure at x = Pressure at y
Unknown Pressure P = P_o + hρg

Determination of density of coconut oil using U tube

First take the water in the U tube then add coconut oil to one of the arm and give some time to settle.After it settles measure the height of coconut oil(h2) and water(h1) from common interface. To take several measurements add coconut oil and measure the heights from the common interface.

First take water and then take coconut oil.Otherwise coconut oil floats in both arms of U tube.
To take several readings we have to add less dense liquid for corresponding arm otherwise always h1 and h2 will be same.
For miscible liquids we cannot use the above method.

Hare’s apparatus

P0 – atmospheric pressure

Arrange the above setup as shown in the figure .Suck the air from the tube,then the liquids in both arm rises upto maximum level.Then measure the heights hw and hl.Then reduce heights and take several sets of reading.

Pascal’s law

Pascal’s law states that a pressure change occurring anywhere in a confined incompressible fluid is transmitted throughout the fluid such that the same change occurs everywhere.

Incompressible fluid means due to the pressure the density of the fluid

The pressure acting on both pistons in a hydraulic jack is equal.

hydraulic lift

The force equation for the small cylinder F_s = p A_s

where F_s = force acting on the piston in the small cylinder (N) , A_s = area of small cylinder (m²) , p = pressure in small and large cylinder (Pa, N/m²)

The force equation for the large cylinder F_l = p A_l

where F_l = force acting on the piston in the large cylinder (N) , A_l = area of large cylinder (m²) , p = pressure in small and large cylinder (Pa, N/m²)

F_s / A_s= F_l / A_l

F_s = F_l A_s/ A_l

Upthrust

A fluid will exert a force upward on a body if it is partly or wholly submerged within it. This is because the deeper into a fluid you go, the greater the weight of it and so the greater the pressure. This difference in pressure between the top and the bottom of the object produces an upward force on it. This is called Upthrust.
- According to Archimedes’ Principle, the upthrust on an object in a fluid is equal to the weight of the fluid displaced.
Upthrust = Weight of Fluid Displaced = mg = vρg

Upthrust = vρg

Archimede’s principle

It states that when a body is fully or partially emerged in an incompressible fluid at rest, it experiences an upward force equal to the weight of the fluid displaced.

When an object is placed on the surface of a liquid it will either float or sink. This depends upon two forces:

The weight W₁ acting vertically downwards, which is due to the gravitational pull of the earth

Upthrust acting vertically upwards, which is equal to the weight of the liquid displaced by the object W₂.

You know that the weight of an object is the product of its volume and its density. Hence,

W₁ = Volume of the object (V) x Density of the object (d₁)

W₂ = Volume of the liquid displaced (V) x Density of the liquid (d₂)

Let us see what are the different situations under which a body floats, sinks or remains submerged completely at any level in the liquid.

Case 1:

When the weight of the object W₁ is equal to the weight of the liquid displaced W₂, the object will stay in the position of rest completely immersed in the liquid. Here,

W₁ = W₂ or

V x d₁ = V x d₂ or d₁ = d₂, then the object will be floating completely immersed in a liquid as shown in figure below.

Weight of the object is equal to the weight of the liquid

Case 2:

When the weight of the object is greater than the weight of the displaced liquid, the object will sink. Here,

Thus, when the density of the object is greater than the density of the liquid, the object will sink.

Weight of the object is greater than the weight of the liquid displaced.

Case 3:-

When the weight of the object is less than the buoyant force (upthrust), the object will float on the surface of the liquid.

When the object floats, only a part of it is submerged in the liquid and volume of the liquid displaced will be less than its own volume. Let V’ be the volume of the liquid displaced by the submerged part of the object. Here

Density of the solid is less than the density of the liquid and hence the object will float.

Weight of the object is less than the weight of the liquid displaced

Hydrometer

Hydrometer is an instrument used for determining the density of a liquid. It usually consists of a glass float with a long thin stem which is graduated. The glass float is a large hollow bulb which increases the buoyancy so that the hydrometer floats. The narrow stem increases the sensitivity of the hydrometer. The bottom of the hydrometer is made heavier by loading it with lead shots so that it floats vertically.

Steady flow All the fluid particles that pass any given point, follow the same path at same speed. In steady flow streamlines never cross each other.

Laminar flow In laminar flow, the velocities of all the particles on any given streamline are equal.

Turbulent flow Above a certain critical speed,fluid become turbulent .It is an irregular flow ,we can’t predict the motion.

Incompressible fluid

In incompressible fluid change in pressure produces no change in density of the fluid. Liquids can be considered incompressible and gases can be considered for small pressure differences.

Viscous force

When two layers of liquid are moving with different velocities they experience tangental forces which tend to retard the faster layer and accelerate the slower layer.These forces are called viscous forces.

Ideal fluid flow means a fluid incompressible,non viscous at streamline flow.

Equation of continuity

If a fluid is undergoing streamline flow then the mass of fluid which enters one end of a tube of flow must be equal to the mass that leaves at the other end during same time.

Example – Equation of Continuity

10 m³/h of water flows through a pipe with 100 mm inside diameter. The pipe is reduced to an inside dimension of 80 mm.

Using equation (2) the velocity in the 100 mm pipe can be calculated

(10 m³/h) (1 / 3600 h/s) = v₁₀₀ (3.14 (0.1 m)² / 4)

or

v₁₀₀ = (10 m³/h) (1 / 3600 h/s) / (3.14 (0.1 m)² / 4)

= 0.35 m/s

Using equation (2) the velocity in the 80 mm pipe can be calculated

(10 m³/h) (1 / 3600 h/s) = v₈₀ (3.14 (0.08 m)² / 4)

or

v₈₀ = (10 m³/h) (1 / 3600 h/s) / (3.14 (0.08 m)² / 4)

= 0.55 m/s

Energy possessed by a fluid

Fluid Kinetic Energy

The kinetic energy of a moving fluid is more useful in applications like the Bernoulli equation when it is expressed as kinetic energy per unit volume

Fluid Potential Energy

The potential energy of a moving fluid is more useful in applications like the Bernoulli equation when is expressed as potential energy per unit volume

Pressure as Energy Density

Pressure in a fluid may be considered to be a measure of energy per unit volume or energy density. For a force exerted on a fluid, this can be seen from the definition of pressure:

Bernoulli’s principle

The Bernoulli Equation can be considered to be a statement of the conservation of energy principle appropriate for flowing fluids.

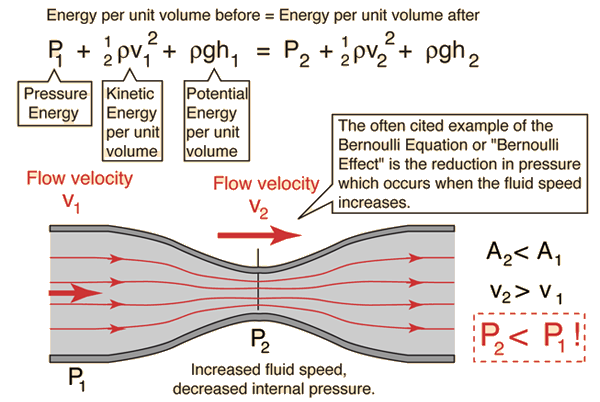
Applications

Bernoulli’s principle can be used to calculate the lift force on an airfoil, if the behaviour of the fluid flow in the vicinity of the foil is known. For example, if the air flowing past the top surface of an aircraft wing is moving faster than the air flowing past the bottom surface, then Bernoulli’s principle implies that the pressure on the surfaces of the wing will be lower above than below. This pressure difference results in an upwards lifting force. Whenever the distribution of speed past the top and bottom surfaces of a wing is known, the lift forces can be calculated (to a good approximation) using Bernoulli’s equations established by Bernoulli over a century before the first man-made wings were used for the purpose of flight. Bernoulli’s principle does not explain why the air flows faster past the top of the wing and slower past the underside. See the article on aerodynamic lift for more info.

The carburettor used in many reciprocating engines contains a venturi to create a region of low pressure to draw fuel into the carburettor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli’s principle; in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.
An injector on a steam locomotive (or static boiler).
The pitot tube and static port on an aircraft are used to determine the airspeed of the aircraft.
The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate, which can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, the continuity equation shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid flow speed. Subsequently, Bernoulli’s principle then shows that there must be a decrease in the pressure in the reduced diameter region. This phenomenon is known as the Venturi effect.

Airfoil

One of the most common everyday applications of Bernoulli’s principle is in air flight. The main way that Bernoulli’s principle works in air flight has to do with the architecture of the wings of the plane. In an airplane wing, the top of the wing is somewhat curved, while the bottom of the wing is totally flat. While in the sky, air travels across both the top and the bottom concurrently. Because both the top part and the bottom part of the plane are designed differently, this allows for the air on the bottom to move slower, which creates more pressure on the bottom, and allows for the air on the top to move faster, which creates less pressure. This is what creates lift, which allows planes to fly. An airplane is also acted upon by a pull of gravity in which opposes the lift, drag and thrust. Thrust is the force that enables the airplane to move forward while drag is air resistance that opposes the thrust force.

Venturi meter

The pressure in the first measuring tube (1) is higher than at the second (2), and the fluid speed at “1” is lower than at “2”, because the cross-sectional area at “1” is greater than at “2”.

A flow of air through a venturi meter, showing the columns connected in a manometer and partially filled with water. The meter is “read” as a differential pressure head in cm or inches of water

The Venturi effect is the reduction in fluid pressure that results when a fluid flows through a constricted section of a pipe.

In fluid dynamics, a fluid’s velocity must increase as it passes through a constriction in accord with the principle of mass continuity, while its static pressure must decrease in accord with the principle of conservation of mechanical energy. Thus any gain in kinetic energy a fluid may accrue due to its increased velocity through a constriction is balanced by a drop in pressure.

By measuring the change in pressure, the flow rate can be determined, as in various flow measurement devices such as venturi meters, venturi nozzles and orifice plates.

Using Bernoulli’s equation in the special case of steady, incompressible, non viscous flows along a streamline, the theoretical pressure drop at the constriction is given by:

p_{1}-p_{2}={\frac {\rho }{2}}\left(v_{2}^{2}-v_{1}^{2}\right)

where $\scriptstyle \rho \,$ is the density of the fluid, $\scriptstyle v_{1}$ is the (slower) fluid velocity where the pipe is wider, $\scriptstyle v_{2}$ is the (faster) fluid velocity where the pipe is narrower (as seen in the figure)

Just before collision
During collision
After collision

Law of conservation of linear momentum

The total linear momentum of a system of interacting bodies on which no external forces are acting remains constant.

Elastic collisions

During collisions, total kinetic energy just before the collision is equal to total kinetic energy just after the collision.

Inelastic collisions

Total kinetic energy is not conserved just before or after collision

Complete inelastic collisions

After the collision both objects move together.

Linear momentum

Linear momentum is a vector quantity defined as the product of an object’s mass m and its velocity v. Linear momentum is denoted by the letter p .

Note that a body’s momentum is always in the same direction as its velocity vector. The units of momentum are kg m/s.

p=mv

Law of conservation of linear momentum

The total linear momentum of a system of interacting bodies on which no external forces are acting remains constant.

Collisions

Let a constant force (f) act in the same direction in which the particle is moving . Initial and final velocities are u and v,time taken – t. 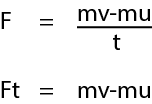Ft is an important quantity in dynamics.It has been named as impulse.

A large force(F) acting in a very small time interval(t) Then Impulse I = F×t

Impulse is a vector quantity.Direction of impulse is the direction of force.

I=Ft=Δ(mv) Unit – kgms^-1

Applications

(i) A cricket player lowers has hands while catching the ball : by doing so the time of impact increases and hence the effect of force decreases.

(ii) When a person falls from a certain height on floor, he receives more injuries as compared to falling on a heap of sand. It is because the Cemented floor does not yield whereas the sand yield there by increasing the time of impact hence decreasing the impact of force.

(iii) The shock absorbers provided in the vehicle helps to travel smoothly on an uneven road. It is because the shockers increases the time of impulse which reduces the force.

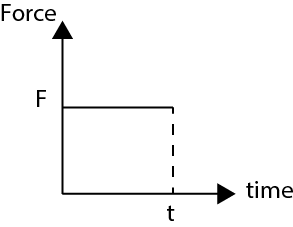In a force – time graph area between the graph and the time axis gives the impulse.

Area=F×t=impulse

Force due to water flow

Conveyor belt

Force on helicopter blades

Projectile Motion Equation

Range Equation for Projectile Motion

Horizontal Projectile Motion

p=mv

Friction

Examples of Rolling Friction

Kinetic friction

Magnitude of Kinetic Friction Fk = μk R Where, Fk = magnitude of kinetic friction R = Normal reaction μk = coefficient of kinetic friction

Static Friction

Static friction is greater in magnitude than kinetic friction in any situation.

Relationship between limiting frictional force and normal reaction

aT=rα

For a single particle of mass m a distance r from the axis of rotation, the moment of inertia is given by I=mr²

L=Iω=constant

Rotational kinetic energy = ½Iω²

Fcentripetal = mrω²

Energy

Kinetic energy

Gravitational potential energy

Elastic potential energy

F = -kx

Conservation of mechanical energy

If we consider atmospheric pressure , say it’s Po , then the pressure at depth h is given by P = Po + hρg

Pascal’s law

Upthrust

Archimede’s principle

Hydrometer

Equation of continuity

Example – Equation of Continuity

Energy possessed by a fluid

Fluid Kinetic Energy

Fluid Potential Energy

Pressure as Energy Density

Bernoulli’s principle

Airfoil

Venturi meter

Law of conservation of linear momentum

Elastic collisions

Inelastic collisions

Complete inelastic collisions

p=mv

A large force(F) acting in a very small time interval(t) Then Impulse I = F×t

I=Ft=Δ(mv) Unit – kgms-1

Magnitude of Kinetic Friction
Fk = μk R
Where,
Fk = magnitude of kinetic friction
R = Normal reaction
μk = coefficient of kinetic friction

a_T=rα

F_centripetal = mrω²

If we consider atmospheric pressure , say it’s P_o , then the pressure at depth h is given by P = P_o + hρg

I=Ft=Δ(mv) Unit – kgms^-1